Estimating the number of species
Estimating the diversity of dinosaurs
Proceedings of the National Academy of Sciences
Published online before print September 5, 2006
Steve C. Wang, and Peter Dodson
Fossil hunters told: Dig deeper
Philadelphia Inquirer, September 5, 2006
Tom Avril
Steve Wang is a statistician at Swarthmore College and Peter Dodson is a paleontologist at the University of Pennsylvania. Their study was widely reported in the media. You can find references to the media coverage and comments by Steve here.
In their paper the authors provided the following description of their results. Here are a few definitions that might be helpful: genera: a collective term used to incorporate like-species into one group, nonavian: not derived from birds, fossiliferous: containing a fossil, rock outcrop: the part of a rock formation that appears above the surface of the surrounding land
Despite current interest in estimating the diversity of fossil and extant groups, little effort has been devoted to estimating the diversity of dinosaurs. Here we estimate the diversity of nonavian dinosaurs at 1,850 genera, including those that remain to be discovered. With 527 genera currently described, at least 71% of dinosaur genera thus remain unknown. Although known diversity declined in the last stage of the Cretaceous, estimated diversity was steady, suggesting that dinosaurs as a whole were not in decline in the 10 million years before their ultimate extinction. We also show that known diversity is biased by the availability of fossiliferous rock outcrop. Finally, by using a logistic model, we predict that 75% of discoverable genera will be known within 60-100 years and 90% within 100-140 years. Because of nonrandom factors affecting the process of fossil discovery (which preclude the possibility of computing realistic confidence bounds), our estimate of diversity is likely to be a lower bound.
In this problem we have a sample of dinosaurs that lived on the earth. These dinosaurs are classified into groups called genera. We can count the number of each generus in our sample. From this we want to estimate the total number of dinosaurs that have roamed the earth. Many different methods for doing this have been developed and the authors of this study use one of the newer methods. We have discussed in prevent Chance News other examples of this problem and it might help to discuss these briefly.
One of the first studies of this kind was suggested by asking similar questions about the number of different species of butterflies in Malaya and was reported in the paper "The relation between the number of species and the number of individuals (1943) by R.A. Fisher, A.S. Corbet and C. B. Williams.(1)
The authors write:
It is the usual experience of collectors of species in a biological group that the species are not equally abundant, even under conditions of considerable uniformity, a majority being comparatively rare while only a few are common. As far as we are aware, no suggestion has been made previously that any mathematical relation existes between the number of individuals and the nummber of species in a random sample of insects or other animals.
Fisher assumed that for a given sample size the number of occurrences of the jth species has a Poisson distribution with mean m, and the m's are independent random variables having an Euler type distribution making the compound distribution a negative binomial distribution . This distribution is then truncated to take into account that the number of species with 0 occurrances is not known. Finally Fisher took a limiting form of this distribution. Using this model the expected number of species with n individuals is:
(1)
<math>\frac{\alpha}{n}x^n. </math> where <math>\alpha </math> and x are parameters obtained as solutions of the equations:
(2)
<math> S = -\alpha log_e(1-x)</math> (3)
<math> N = \frac{\alpha x}{(1-x)}.</math> Here S is the sample size and N the number of species observed.
Thus the expected number of species with n individual can be represented as a harmonic series of the form
<math> n_1, \frac{n_1}{2} x, \frac{n_1}{3} x^2,\frac{n_1}{4} x^3,.....,etc.</math> From this it follows that the total number of species expected is:
<math> -\alpha log_e(1-x).</math> and the expected number of individuals is
<math> -\frac{\alpha x}{1-x}</math> To see how Fisher's model fits the observed data the authors use only the rairer species that were represented less than 25 times. With this limitation there are N of = 3306 individuals S = 501 species.
Then putting S = 501 and N = 3306 we can use equations (2) and (3) to solve for \alpha and x. Doing this we find that <math> x = .95268 and \alpha = 164.21</math> Using equation (1) we can find the expected number of species that appear i times for i = 1 to 24 and compare these with the observed numbers. The results are shown in the following table.
Our table differs from the corresponding table in the authors article becase they obtained a different value for x and <math>\alpha</math> but we believe that our values are correct.
Wang and Dodson were interested in finding the number of species (in their case genera) that have not been observed in previous samples. This problem was first studied in a paper by I.J. Good (1953): "The population frequencies of species the estimation of population parameters." (2) and by I.J. Good and G. H. Tollmin (1956) in the paper "The number of new species and the increase in population coverage, when a sample is increased (3).
Bradley Efron and Ronald Thisted used the methods developed by Good and Tollmin to answer two questions provided in the titles of the two papers they wrote; (1976) "Estimating the number of unseen species (4). and (1987) How many words did Shakespeare know?"
Efron and Thisted considered the words in Shakespeare's as species and took as the first sample Shakespear's know works which comprised of 884,647 using their convention for when two words are different they found 31,534 different words. They provided a table showing the number of words that accored once, twice, three times ect. up to 100. Following Fisher, they assumed that for the first sample the number of times that a word occurs s has a Poisson distribution with mean <math>\lambda_s</math> which is proportional to the size of the sample. Like Fisher they assumed that <math>\lambda_s</math> is a random variable but unlike Fisher they did not assume that they knew its distribution but rather used an imperical distribution obtained from the data. They then consider a second sample with sample size a multiple t of the first sample and calcultate the expected number of words that will occur in this sample that did not occur in the first sample. They find that if they take a sample the size of his known works the expected number of new words would be 11,430 which can be considered to be a lower bound on the number of additional words that Shakespeare knew.
In their second paper Efron and Thisted use their results to help decide if a new poem found in 1985 by Shakesperean scholar Gary Taylor was written by Shakespeare. This poem had 429 words with 258 being distinct. The authors ranked the 258 distinct words in order of rairity of usage in Shakespeares known works. They found that 9 of the words were never used by Shakespeare. They estimated that if Shakespeare were to write new work with 429 words the expected number of new words would be 6.97. They develop other similar tests and apply them to this new poem as well as to similar size poems known to be written by well known authors of the same period as Shakspeare. They conclude "On balance, the poem is found to fit previous Shakespearean usage reasonably well.
Another esample of estimating the number of species more in the spirit of the Dinosaur study was carried out by Charles Paxton of Oxford University and reported in a paper "A cumulative species description curve for large open water marine animals" (6)
Paxton estimated the number of yet undiscovered salt water species whose length exceeds 2 meters. By 1995, the number of such species identified had reached 217, but the rate of new finds has been decreasing. By examining the pattern of discoveries over the years 1830-1995, Paxton estimates that 47 such species remain to be found. He did this by constructing the following species accumulation curve for these large marine animals from 1830 to 1995.
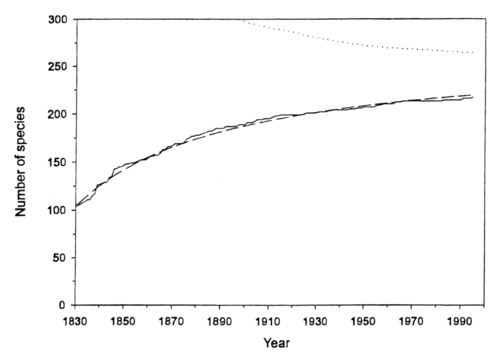
Number of described large open water fauna (>2m length/width)
since 1830 (-), cummulative number of species discribed;(-----), the
expected cummulative number of species from the model;(.....), successive estimates of the maximum number of species > 2m long.
.
Finally we come to the method used by Wang and Dodson to estimate the number of species dinasours that have not been discovered. This method developed by Anne Chao and Shen-Ming Lee in their paper "Estimating the number of classes via sample coverage". The concept of sample coverage was introduced by I.J. Good in his 1953 paper (2).
We use the term classes rather than species since this will include species, genera, words ect. We imagine a population of classes indexed by 1,2... N and we want to estimate N based on a sample from the classes. Let <math>p_i</math> be the probability that any observation belongs to the ith class and X_i be the number of elements of the ith class observed in the sample (i = 1,...., N). Then (X_1, X_2,..., X_N) has a multnomial distribution. Let f_i be the number of classes that have exactly i elements in the sample for i = 1 to n with n the size of the sample. We want to estimate N from the knowledge of f_i.
References
(1) Fisher R.A.; Corbet; C.B. Williams C.B. (1943), "The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population." Journal of Animal Ecology, 12, 42-58. (Available from Jstor).
(2) Good, I. J (1953) "On the population freqencies of species and the estimation of population parameters," Biometrika, 40, 2137-264.
(3) Good I.J. and Toulmin (G) (1956) "The number of new species, and the increase in population coverage when a sample is increased", Biometrika, 43, 45-63.
(4) Thisted, R., and Efron, B (1976) "Estimating the Number of unseen species: How many words did Shakespeare know?" Biometrika, 63,(1976) 435-447.
(5) Thisted, R, and Efron, B (1987), "Did Shakespear write a newly discovered poem?" Biometrika, 74 (1986), 445, 445-455 .
(6) Paxton, C.G.M. (1998), "A cumulative species description curve for large open water marine animals". Journal of the Marine Biological Association of the UK, 78, 1389-1391.