Chance News 92
Quotations
"I've done the calculation and your chances of winning the lottery are identical whether you play or not."
Suggested by Naomi Neff (with thanks to Cynthia Slater)
"As much as it pleases me to see statistical data introduced in the Supreme Court, the act of citing statistical factoids is not the same thing as drawing sound inferences from them."
Submitted by Paul Alper
Forsooth
“The quants have arrived at the Academy [of Motion Picture Arts and Sciences]. …. The goals in making ... predictions extend beyond [Oscar night]. Dr. Rothschild [Microsoft Research economist] is testing whether surveying people online about Oscar patterns—for example, does winning best-adapted screenplay correspond with winning best picture?—is a method that can be translated to forecasting in other areas. If it works, ‘We can apply it to all sorts of other things we don't have data for,’ Dr. Rothschild said."
by Carl Bialik, The Wall Street Journal, February 23, 2013
Submitted by Margaret Cibes
Simpson’s paradox and the ecological fallacy
The lay public tends to believe that statistics is merely a (rather dull) branch of mathematics. In fact, the discipline of statistics should be viewed as a science, as exemplified by physics, astronomy, chemistry, etc., which uses mathematics extensively and is situation dependent. In other word, the same numbers lead to different conclusion depending on the context.
Prime examples of situation dependency may be found in the discussions of Simpson’s paradox and the even more subtle phenomenon known as the ecological fallacy. A treatment of the former can sometimes be found in elementary statistics textbooks but the latter, being less intuitive, is relatively rare in textbooks but often pops up in learned discussions where the reader is warned about drawing false conclusions.
The dating of the phenomenon now known as Simpson’s paradox goes back before any of the current Chance News readers were born; the bestowing of the name, according to Wikipedia, originated much later in 1971:
Simpson's paradox (or the Yule–Simpson effect) is a paradox in which a trend [i.e., inequality] that appears in different groups of data disappears when these groups are combined, and the reverse trend [i.e., opposite inequality] appears for the aggregate data. This result is often encountered in social-science and medical-science statistics, and is particularly confounding when frequency data are unduly given causal interpretations.
The Wikipedia article has this “real-life example from a medical study comparing the success rates of two treatments for kidney stones.”
| Treatment A | Treatment B | |
|---|---|---|
| Small Stones | Group 1 93% (81/87) |
Group 2 87% (234/270) |
| Large Stones | Group 3 73% (192/263) |
Group 4 69% (55/80) |
| Both | 78% (273/350) | 83% (289/350) |
The paradoxical conclusion is that treatment A is more effective when used on small stones, [93% > 87%] and also when used on large stones, [73% > 69%] yet treatment B is more effective when considering both sizes at the same time [78% < 83%]. In this example, the "lurking" variable (or confounding variable) of the stone size was not previously known to be important until its effects were included.
In this context of kidney stones, it is clear that disaggregation makes sense and Treatment A is preferable to Treatment B despite Treatment B being better in the aggregate sense. However, if we take the same numbers but change the context to Athletic Team A and Athletic Team B who play Small and Large opponents and the only thing that determines ranking is the total winning percentage, then Athletic Team B is preferred to Athletic Team A. That is, aggregation makes sense in this scenario as it did not in the original Wikipedia presentation.
Other interesting examples are provided in the Wikipedia article. When money is at stake, as in the “Berkeley gender bias” case discussed in Wikipedia, finding a lurking (confounding) variable requires some clever slicing to find “Small” and “Large” which will reverse the inequality. The Wikipedia article also refers to the so-called “low birth rate paradox” whereby “it has been observed that babies of low birth weights born to smoking mothers have a lower mortality rate than the babies of low birth weights of non-smokers.” The paradoxical implication is that smoking helps to lower mortality of newborns. More on this below.
A different Wikipedia article has two definitions of the ecological fallacy. The first definition focuses on aggregation and disaggregation. With this definition, Simpson’s paradox is subsumed under the ecological fallacy:
An ecological fallacy (or ecological inference fallacy) is a logical fallacy in the interpretation of statistical data where inferences about the nature of individuals [disaggregation] are deduced from inference for the group [aggregation] to which those individuals belong.
The second definition spotlights the notion of correlation:
Ecological fallacy can refer to the following statistical fallacy: the correlation between individual variables is deduced from the correlation of the variables collected for the group to which those individuals belong.
Although elementary statistics textbooks do not customarily mention the ecological fallacy, it is even older than Simpson’s paradox. The term was first coined in 1950 by William Robinson but goes back to Emile Durkheim’s 1897 study of suicide. From the graph, it appears that the greater the proportion of Protestants, the greater is the suicide rate:
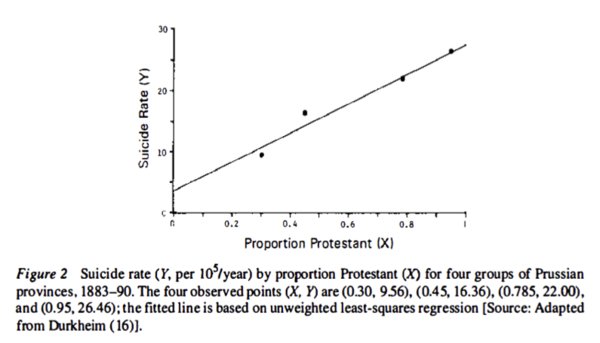
According to Morgenstern, the estimated rate ratio of 7.6 was probably not because suicide rates were nearly 8 fold higher in Protestants than in non-Protestants. Rather, because none of the regions was entirely Protestant or non-Protestant, it may have been non-Protestants (primarily Catholics) who were committing suicide in predominantly Protestant provinces. It is plausible that members of a religious minority might have been more likely to commit suicide than were members of the majority. Living in a predominantly Protestant area had a contextual effect on suicide risk among Catholics.
Interestingly, Morgenstern points out that Durkheim compared the suicide rates at the individual level for Protestants, Catholics and Jews living in Prussia, and from his data, the rate was about twice as great in Protestants as in other religious groups. Thus, when the rate ratios are compared (2 vs 8), there appears to be substantial ecological bias using the aggregate level data.
In the above situation there was no reversal of an inequality, merely a sharp diminishing from aggregated to disaggregated. The following example of the ecological fallacy actually illustrates the reversal.
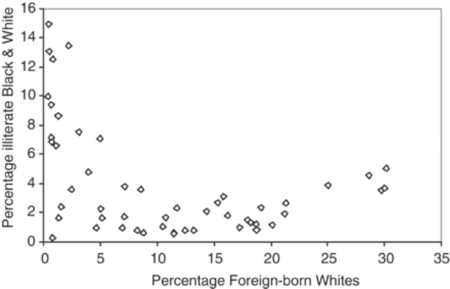
One compelling example by Robinson (1950), was the relationship between nativity (foreign vs native born) and literacy. For each of the 48 states in the USA of 1930, [there were only 48 states admitted to the Union by 1930] Robinson computed two numbers: the percent of the population who were foreign-born (i.e. immigrants), and the percent who were literate. He found the correlation between the 48 pairs of numbers was .53. This ecological correlation suggested a positive association between foreign birth and literacy: the foreign-born (immigrants) are more likely to be literate than the native-born. In reality, the association was negative: the correlation computed at the individual level was −0.11 (immigrants were less literate than native citizens). The ecological correlation gave the incorrect inference. This is because the foreign-born (immigrants) tended to migrate to and settle in states where the native-born are relatively literate. In this example by Robinson, the correlation is totally reversed.
Robinson’s data look this way:
The following graph dealing this time with income and being foreign born is even more striking:
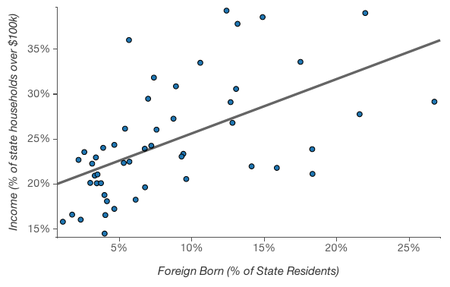
U.S. states with proportionally more immigrants have proportionally more households with income above $100k. Ergo, immigrants are more likely than non-immigrants to have household incomes above $100k.
Hopefully something feels off about that logic. Because it’s wrong. Actually the relationship between income and being an immigrant at the individual level is the opposite.
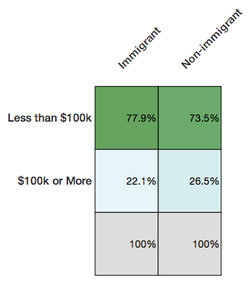
Deducing from the first chart that immigrants are more likely to be well-off is committing the ecological fallacy—attributing qualities at the individual level because of a relationship at a group level.
But here is a more recent and more difficult-to-unravel ecological fallacy:
That example was pretty easy to catch, not least because it feels intuitive that immigrants would tend to have lower income than non-immigrants.
But not all ecological fallacies are so easy to spot. For example, there’s a negative correlation between per capita income in a state and the percent of the 2012 presidential election vote that went to Romney.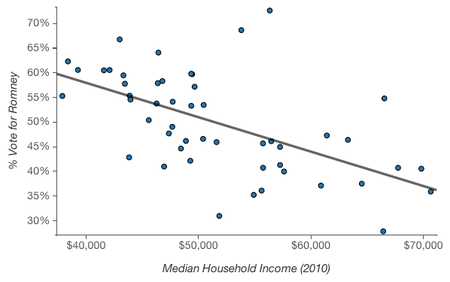
It’s easy to picture rich and liberal cities like San Francisco and New York, hear the phrase “latte liberal” a couple times, and believe that higher income is in fact correlated with voting Democratic. At an individual level, though, higher income is associated with voting Republican.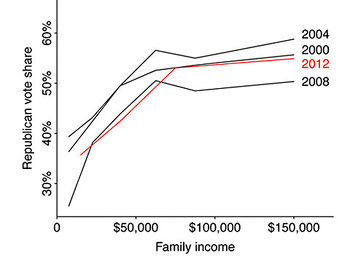
The (simplified) explanation for this apparent paradox? Across the country, lower income folk tend to vote Democrat; within blue states, upper income folk also vote Democrat, but in red states they vote Republican.
A general way to look at where the fallacy might arise is via the following graph and explanation of Durkheim’s suicide data:

That is, within every group it is possible that even if the correlation (regression line) is negative, it can happen that across the groups, the correlation (regression line) is positive. Note too that in many situations the “within” is not a cloud of points, each of which represents an individual, but instead, there is just one point, average exposure and average outcome. Further, exposure may come from one data base and outcome from another data base. This is totally unlike the kidney stones example which began this wiki because there stone and success can be tied to a particular individual.
Discussion
1. An oft-used synonym for the ecological fallacy (inferring from group to individuals) is called cross level inference. The opposite of the ecological fallacy is the atomistic fallacy (inferring from the individuals to the group).
2. With regard to Robinson’s data, besides the fallacy aspect, what is wrong with doing a correlation in the first place?
3. Concerning the graph of foreign born and income, suppose the ordinates were interchanged. How is this then similar to Durkheim’s study and its ecological fallacy? 4. The paradox of the smoking mother is supposedly explained by the following:
The birth weight distribution for children of smoking mothers is shifted to lower weights by their mothers' actions. Therefore, otherwise healthy babies (who would weigh more if it were not for the fact their mother smoked) are born underweight. They have a lower mortality rate than children who have other medical reasons why they are born underweight, regardless of the fact their mother does not smoke. In short, smoking may be harmful in that it contributes to low birth weight, but other causes of low birth weight are generally more harmful only with regard to their weight.
How does this explanation accord with the aforementioned phrase, situation dependent?
Submitted by Paul Alper
Normal vs. paranormal
John Allen Paulos sent a link to the following cartoon, reproduced below as presented on the StackExchange blog Cross Validated:
From: A visual comparison of normal and paranormal distributions
Matthew Freeman J Epidemiol Community Health 2006;60:6.
Lower caption says 'Paranormal Distribution'- no idea why the graphical artifact is occuring.