Chance News 83
Quotations
“A poll is not laser surgery; it’s an estimate.”
ABC Blogs, December 3, 2007
Submitted by Margaret Cibes
"The most famous result of Student’s experimental method is Student’s t-table. But the real end of Student’s inquiry was taste, quality control, and minimally efficient sample sizes for experimental Guinness – not to achieve statistical significance at the .05 level or, worse yet, boast about an artificially randomized experiment."
(Ziliak is the co-author of The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives. You can find a review of this book by David Aldous on amazon.com)
Submitted by Bill Peterson
“[W. S. Gossett] wrote to R. A. Fisher of the t tables, "You are probably the only man who will ever use them (Box 1978)."
“[W]e see the data analyst's insistence on ‘letting the data speak to us’ by plots and displays as an instinctive understanding of the need to encourage and to stimulate the pattern recognition and model generating capability of the right brain. Also, it expresses his concern that we not allow our pushy deductive left brain to take over too quickly and perhaps forcibly produce unwarranted conclusions based on an inadequate model.”
Technometrics, February 1984
Thomas L. Moore recommended this article in an ISOSTAT posting. (It is available in JSTOR.)
We are familiar with George Box’s famous statement: “All models are wrong but some are useful.” Here is another variant, cited in Wikipedia:
- “Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.”
Submitted by Margaret Cibes
(Note. For an interesting recent discussion revisiting this theme, see All models are right, most are useless on Andrew Gelman's blog, 4 March 2012).
“There are two kinds of statistics: the kind you look up and the kind you make up.”
Submitted by Paul Alper
“Definition of Statistics: The science of producing unreliable facts from reliable figures.”
"The only science that enables different experts using the same figures to draw different conclusions."
Submitted by Paul Alper
“Science involves confronting our `absolute stupidity'. That kind of stupidity is an existential fact, inherent in our efforts to push our way into the unknown. …. Focusing on important questions puts us in the awkward position of being ignorant. One of the beautiful things about science is that it allows us to bumble along, getting it wrong time after time, and feel perfectly fine as long as we learn something each time. …. The more comfortable we become with being stupid, the deeper we will wade into the unknown and the more likely we are to make big discoveries.”
Journal of Cell Science, 2008
Submitted by Margaret Cibes
Forsooth
“In the first four months [at the new Resorts World Casino New York City], roughly 25,000 gamblers showed up every day, shoving a collective $2.3 billion through the slots and losing $140 million in the process. …. Resorts World offers more than 4,000 slot machines, but thanks to state law, there are no traditional card tables.”
The Wall Street Journal, February 18, 2012
Submitted by Margaret Cibes
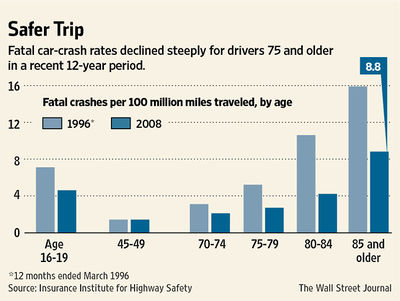
“Drivers 85 and older still have a higher rate of deadly crashes than any other age group except teenagers.”
(The article also describes two women who have learned to "compensate" for their macular degeneration in various ways - not necessarily welcome news!)
The Wall Street Journal, February 29, 2012
Submitted by Margaret Cibes
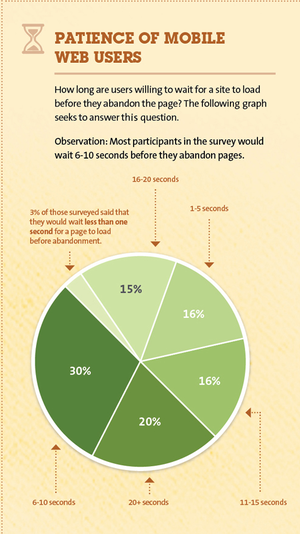
See the "Observation" at the top of the chart.
“The Meaning of most”, downloaded from Junk Charts, March 1, 2012
Submitted by Margaret Cibes
“Here is the rub: Apple is so big, it’s running up against the law of large numbers. Also known as the golden theorem, with a proof attributed to the 17th-century Swiss mathematician Jacob Bernoulli, the law states that a variable will revert to a mean over a large sample of results. In the case of the largest companies, it suggests that high earnings growth and a rapid rise in share price will slow as those companies grow ever larger.”
The New York Times, February 24, 2012
Bill Peterson found Andrew Gelman’s comments[1] about this article.
Submitted by Margaret Cibes
Kaiser Fung on Minnesota’s ramp meters
A number references to Kaiser Fung’s book, Numbers Rule Your World, appear in Chance News 82. From a Minnesotan’s point of view, however, the most important topic he discusses is not hurricanes, not drug testing, and not bias in standardized testing. Rather, the most critical issue is ramp metering as a means of improving traffic flow, relieving congestion and reducing travel time on Minnesota highways. “Industry experts regard Minnesota’s system of 430 ramp meters as a national model.”
Unfortunately, “perception trumped reality.” An influential state senator, Dick Day, now a lobbyist for gambling interests, “led a charge to abolish the nationally recognized program, portraying it as part of the problem, not the solution.”
Leave it to Senator Day to speak the minds of “average Joes”--the people he meets at coffee shops, county fairs, summer parades, and the stock car races he loves. He saw ramp metering as a symbol of Big Government strangling our liberty.
In the Twin Cities, drivers perceived their trip times to have lengthened [due to the ramp meters] even though in reality they have probably decreased. Thus, when in September 2000, the state legislature passed a mandate requiring MnDOT [Minnesota Department of Transportation] to conduct a “meters shutoff” experiment [of six weeks], the engineers [who devised the metering program] were stunned and disillusioned.
To make a long story short, when the ramp meters came back on, it turns out that:
[T]he engineering vision triumphed. Freeway conditions indeed worsened after the ramp meters went off. The key findings, based on actual measurements were as follows:
- Peak freeway volume dropped by 9 percent.
- Travel times rose by 22 percent, and the reliability deteriorated.
- Travel speeds declined by 7 percent.
- The number of crashes during merges jumped by 26 percent.
“The consultants further estimated that the benefits of ramp metering outweighed costs by five to one.” Nevertheless, the-above objective measures had to continue to battle subjective ones:
Despite the reality that commuters shortened their journeys if they waited their turns at the ramps, the drivers did not perceive the trade-off to be beneficial; they insisted that they would rather be moving slowly on the freeway than coming to a standstill at the ramp.
Accordingly, the engineers decided to modify the optimum solution to take into account driver psychology. “When they turned the lights back on, they limited waiting time on the ramps to four minutes, retired some unnecessary meters, and also shortened the operating hours.” Said differently, the constrained optimization model the engineers first considered left out some pivotal constraints.
Discussion
1. Do a search for “behavioral economics” to see the prevalence of irrational perceptions and subjective calculations in the economic sphere.
2. Fung discusses an allied, albeit inverse, problem of waiting-time misconception. This instance concerns Disney World and its popular so-called FastPass as a means of avoiding queues. According to Fung
Clearly, FastPass users love the product--but how much waiting time can they save? Amazingly, the answer is none; they spend the same amount of time waiting for popular rides with or without FastPass!..So Disney confirms yet again that perception trumps reality. The FastPass concept is an absolute stroke of genius; it utterly changes perceived waiting times and has made many, many park-goers very, very giddy.
3. An oft-repeated and perhaps apocryphal operations research/statistics/decision theory anecdote has to do with elevators in a very large office building. Employees complained about excessive waiting times because the elevators all too frequently seemed to be in lockstep. Any physical solution such as creating a new elevator shaft or installing a complicated timing algorithm would be very expensive. The famous and utterly inexpensive psychological solution whereby perception trumped reality was to put in mirrors so that the waiting time would seem less because the employees would enjoy admiring themselves in the mirrors. Note that older and more benighted operations research/statistics/decision theory textbooks would have used the word “women” instead of “employees” in the previous sentence.
4. A very modern and frustrating example of perception again trumping reality can often be observed in supermarkets which have installed self-checkout lanes without placing a limit on the number of items per shopper. In order to avoid a line at the regular checkout, some shoppers with an extremely large number of items will often choose the self-checkout and take much longer to finish than if had they queued at the regular checkout. Explain why said shoppers psychologically might prefer to persist in that behavior despite evidence to the contrary. Why don’t supermarkets simply limit the number of items per customer at self-checkout lanes?
Submitted by Paul Alper
Don’t forget Chebyshev
Super Crunchers, by Ian Ayres, Random House, 2007
When I taught at Stanford Law School, professors were required to award grades that had a 3.2 mean. …. The problem was that many of the students and many of the professors had no way to express the degree of variability in professors’ grading habits. …. As a nation, we lack a vocabulary of dispersion. We don’t know how to express what we intuitively know about the variability of a distribution of numbers. The 2SD [2 standard-deviation] rule could help give us this vocabulary. A professor who said that her standard deviation was .2 could have conveyed a lot of information with a single number. The problem is that very few people in the U.S. today understand what this means. But you should know and be able to explain to others that only about 2.5 percent of the professor’s grades are above 3.6. [pp. 221-222]
Discussion
1. Suppose that a professor's awarded grades had mean 3.2 and SD 0.2.
(a) Under what condition could we say that “only about 2.5 percent of the professor’s grades are above 3.6”?
(b) Without that condition, what could we say, if anything, about the percent of awarded grades outside of a 2SD range about the mean? About the percent of awarded grades above 3.6?
2. Suppose that a professor's raw grades had mean 3.2 and SD 0.2. Do you think that this would be a realistic scenario in most undergraduate college classes? In most graduate-school classes? Why or why not?
3. How could a professor construct a distribution of awarded grades with mean 3.2 and SD 0.2, based on raw grades, so that one could say that only about 2.5 percent of the awarded grades are above 3.6? What effect, if any, could that scaling have had on the worst – or on the best – raw grades?
Submitted by Margaret Cibes
Critique of women-in-science statistics
“Rumors of Our Rarity are Greatly Exaggerated: Bad Statistics About Women in Science”
by Cathy Kessel, Journal of Humanistic Mathematics, July 2011
Based on her apparently extensive and detailed study of reports about female-to-male ratios with respect to STEM abilities/careers, Kessel discusses three major problems with the statistics cited in them, as well as with the repetition of these questionable figures in subsequent academic and non-academic reports.
Whatever their origins, statistics which are mislabeled, misinterpreted, fictitious, or otherwise defective remain in circulation because they are accepted by editors, readers, and referees.
“The Solitary Statistic.” A 13-to-1 boy-girl ratio in SAT-Math scores has been widely cited since it appeared in a 1983 Science article. That ratio was based on the scores of 280 seventh- and eighth-graders who scored 700 or above on the test over the period 1980-83. These students were part of a total of 64,000 students applying for a Johns Hopkins science program for exceptionally talented STEM-potential students. Kessel faults the widespread references to this outdated data, among other issues, and she cites more recent statistics at Hopkins and other such programs, including a ratio as low as 3 to 1 in 2005.
“The Fabricated Statistic.” A “finding” that “Women talk almost three times as much as men” was published in The Female Brain in 2006. This was supposed to explain why women prefer careers which allow them to “connect and communicate” as opposed careers in science and engineering. Kessel outlines some issues that might make this explanation questionable.
“The Garbled Statistic.” An example from “The Science of Sex Differences in Science and Mathematics,” published in Psychological Science in the Public Interest in 2007, was a report that women were “8.3% of tenure-track faculty at ‘elite’ mathematics departments.” A 2002 survey produced similar math data; that survey was based on the “top 50 departments.” These and other reports generally reported only the aggregate figure and not any of the raw data by rank. Kessel gives other examples in which raw data summary tables (which she had requested and received) would have been helpful to interpreting results.
Although noticing mistakes may require numerical sophistication or knowledge of particular fields, accurate reporting of names, dates, and sources of statistics does not take much skill. At the very least, authors and research assistants can copy categories and sources as well as numbers. Editors can (and should) ask for sources.
Discussion
1. Is there anything random about the group of students applying to a university’s program for talented students - or about the top SAT-M scorers in that group? Why are these important questions?
2. Kessel quotes a statement that has been reported a number of times: “Women use 20,000 words per day, while men use 7,000." How do you think the researchers got these counts?
3. Why might it be important to consider academic rank as a variable in analyzing the progress, or lack thereof, of women in obtaining university positions?
4. Why might it be important to know more about the sponsorship of these studies – researcher affiliations, funding, etc.?
Submitted by Margaret Cibes, based on a reference in March 2012 College Mathematics Journal
Ethics study of social classes
“Study: High Social Class Predicts Unethical Behavior”
The Wall Street Journal, February 27, 2012
Here is an abstract of the study[2] referred to in the article:
Seven studies using experimental and naturalistic methods reveal that upper-class individuals behave more unethically than lower-class individuals. In studies 1 and 2, upper-class individuals were more likely to break the law while driving, relative to lower-class individuals. In follow-up laboratory studies, upper-class individuals were more likely to exhibit unethical decision-making tendencies (study 3), take valued goods from others (study 4), lie in a negotiation (study 5), cheat to increase their chances of winning a prize (study 6), and endorse unethical behavior at work (study 7) than were lower-class individuals. Mediator and moderator data demonstrated that upper-class individuals’ unethical tendencies are accounted for, in part, by their more favorable attitudes toward greed.
See also "Supporting Information", published online in Proceedings of the National Academy of Sciences of the USA, February 27, 2012.
Discussion
1. If you were going to write an article about this study, and you had access to the entire report, what would be the first, most basic, information you would want to provide to your readers about the “class” categories referred to in the abstract?
2. The article indicates that the sample sizes for the first three experiments were “250,” “150 drivers,” and “105 students.” Besides the relatively small sample sizes, what other issues can you identify as a potential problems in making any inference about ethics from these experimental results?
Submitted by Margaret Cibes
Judea Pearl wins Turing Prize
Danny Kaplan posted a link to this story on the Isolated Statisicians e-mail list:
A Turing Award for helping make computers smarter.
by Steve Lohr, Bits blog, New York Times, 15 March 2012
Judea Pearl of UCLA has been awarded the 2012 Turing Prize by the Association for Computing Machinery. As described in the NYT article, Pearl's work on probabilistic reasoning and Bayesian networks has influenced applications in areas from search engines to fraud detection to speech recognition.
Danny's message provided links to Pearl's web page for references to his work on causality, and to this talk, "The Art and Science of Cause and Effect," which is the epilogue to his famous book, Causality.
Danny's own Statistical Modeling textbook includes a chapter which discusses some of these ideas at a level appropriate for an introductory statistics audience.
A bizarre anatomical correlation
Politicians Swinging Stethoscopes, Gail Collins, The New York Times, March 16, 2012.
When a topic carries strong emotions, often people forget to check their facts carefully. And abortion is possibly the most emotional topic in politics today. It's not too surprising that opponents of abortion have tried to promote a link between abortion and breast cancer.
New Hampshire, for instance, seems to have developed a thing for linking sex and malignant disease. This week, the State House passed a bill that required that women who want to terminate a pregnancy be informed that abortions were linked to "an increased risk of breast cancer." As Terie Norelli, the minority leader, put it, the Legislature is attempting to make it a felony for a doctor "to not give a patient inaccurate information."
This was actually an issue about 25 years ago, when C. Everett Koop was Surgeon General. The American Cancer Society (ACS) has written that scientific research studies have not found a cause-and-effect relationship between abortion and breast cancer, and cites a comprehensive review in 2003 by the National Cancer Institute (NCI). But numerous pro-life sites still claim the opposite, with headlines like Hundreds of Studies Confirm Abortion-Breast Cancer Link.
It is interesting to speculate why pro-life sites would promote the abortion/breast cancer link so strongly in spite of dismissive commentary from respected organizations like ACS and NCI. If you believe that abortion is murder (as many people do), then it is not too far a leap to believe that something this evil would necessarily carry bad health consequences at the same time. It may also be a belief that mainstream organizations like ACS and NCI are dominated by pro-abortion extremists.
It is still curious, because if abortion is immoral, it should not matter whether it has bad side effects, such as an increased risk of breast cancer, or good side effects, such as a decrease in the crime rate. It may be that opponents of abortion feel free to use any weapon at their disposal to dissuade women from choosing abortion. It is worth noting that opponents of abortion are not the first and will not be the last group that has seized on a dubious statistical finding to support their political perspective.
The abortion/breast cancer link at least has biological plausibility. The number of pregnancies that you have and the number of live births are indeed associated with various types of cancer, so it is not too far fetched to believe that abortion might be related to these cancers as well. But another cancer link in an area almost as contentious lacks even this biological plausibility.
And there’s more. One of the sponsors, Representative Jeanine Notter, recently asked a colleague whether he would be interested, "as a man," to know that there was a study "that links the pill to prostate cancer."
Clearly, Ms. Notter understands that only women consume birth control pills and that only men have a prostate. What she is claiming is
that nations with high use of birth control pills among women also tended to have high rates of prostate cancer among men.
Gail Collins mocks this correlation.
You could also possibly discover that nations with the lowest per capita number of ferrets have a higher rate of prostate cancer.
Birth control pills are possibly associated with ovarian and cervical cancer, and these are two organs that women do have. They may also be associated with a decrease in the risk of endometrial cancer. If you don't believe that NCI is overrun by extremists, you might find this fact sheet to offer a helpful review of these risks. Disentangling these cancer risks from other confounders (such as the age at first sexual intercourse) is very difficult.
Submitted by Steve Simon
Questions
1. What is the name for the type of study that notes that "nations with high use of birth control pills among women also tended to have high rates of prostate cancer among men"?
2. Randomized studies of the link between abortion and breast cancer are clearly impossible. What types of observational studies might be used to examine this link? What are the strengths and weaknesses of those types of studies.
Playing the casino
“The Man Who Broke Atlantic City”
by Mark Bowden, The Atlantic, April 2012
This is the story of an extremely talented blackjack player who is now banned from many casinos – not because of card-counting (supposedly) but because he was able to negotiate terms of play that lowered the house advantage.
Fifteen million dollars in winnings from three different casinos? .... How did he do it? .... The wagering of card counters assumes a clearly recognizable pattern over time, and Johnson was being watched very carefully. The verdict: card counting was not Don Johnson’s game. .... As good as he is at playing cards, he turns out to be even better at playing the casinos. ....
Sophisticated gamblers won’t play by the standard rules. They negotiate. Because the casino values high rollers more than the average customer, it is willing to lessen its edge for them ... primarily by offering ... discounts .... When a casino offers a discount of, say, 10 percent, that means if the player loses $100,000 at the blackjack table, he has to pay only $90,000. ….
So how did all these casinos end up giving Johnson ... a “huge edge”? “I just think somebody missed the math when they did the numbers on it,” he told an interviewer.
Johnson did not miss the math. For example, at the [Tropicana], he was willing to play with a 20 percent discount after his losses hit $500,000, but only if the casino structured the rules of the game to shave away some of the house advantage. Johnson could calculate exactly how much of an advantage he would gain with each small adjustment in the rules of play. He won’t say what all the adjustments were …, but they included playing with a hand-shuffled six-deck shoe; the right to split and double down on up to four hands at once; and a “soft 17”…. [H] whittled the house edge down to one-fourth of 1 percent …. In effect, he was playing a 50-50 game against the house, and with the discount, he was risking only 80 cents of every dollar he played. He had to pony up $1 million of his own money to start, but …: “You’d never lose the million. If you got to [$500,000 in losses], you would stop and … owe them only $400,000.” ….
The Trop has embraced Johnson, inviting him back to host a tournament—but its management isn’t about to offer him the same terms again.
Submitted by Margaret Cibes
PFO
Sobering reminder: just because it is intuitively obvious doesn’t mean it’s true
by Harold DeMonaco, HealthNewsReview.org, 23 March 2012
According to DeMonaco, all of us are born with PFO, patent foramen ovale (an opening between the right and left atria or upper chambers in the heart). “It allows blood to bypass the lungs in the fetus since oxygen is supplied by the mother’s blood circulation. The PFO closes in most right after birth.”
When the PFO doesn’t close properly, “There is good evidence that a significant number” of strokes result.
In theory, blood clots can travel from the right side of the heart and into the left ventricle and then be carried to the brain causing the stroke. Based on a number of reported case studies and small open label trials, a number of academic medical centers began to provide a new catheter based treatment. The treatment consists of placement of a closure device into the heart through the veins and serves to seal the opening. The procedure looks much like a cardiac catheterization. There are at least three medical devices used during this procedure; the Amplatzer PFO occluder, the Gore Helix Septal Occluder and the Starflex Septal Repair Implant.
In what HealthNewsReview.org refers to as a “Sobering reminder: just because it is intuitively obvious doesn’t mean it’s true,”
The industry sponsored study reported this week [in the March 15, 2012 NEJM] looked at two approaches to managing people who have had a previous cryptogenic stroke: 462 had medical care consisting of warfarin, aspirin or both for two years. 447 had placement of a Starflex Implant along with clopidogrel for 6 months and aspirin for two years. All subjects were randomized to the treatment arms. At the end of two years, 2.9% of the PFO closure group suffered another stroke compared to 3.1% of the people treated with drugs alone. Basically no difference in stroke outcome.
Overall, adverse events were equal in both groups with those having the device implanted suffering more events directly related to its placement.
Discussion
1. The catheter-based treatments had been deemed successful via so-called “open label” trials. Google open label trials to see why that type of clinical trial doesn’t carry the clout of some other types of clinical trials. This NEJM “study took 9 years to complete. A major reason for delay in completion was the inability of many centers to enroll patients. Since the closure devices are commercially available, they are routinely used off label. Patients had little reason to enroll in a clinical trial.”
2. Note the pun in The March 15 2012 issue of the New England Journal of Medicine, whose editorial comment which accompanied the article: “Patent Foramen Ovale Closure — Closing the Door Except for Trials.”
3. One of the manufacturers of the catheter, Starflex, was also involved in another PFO catheter procedure for alleviating migraines, the so-called MIST trial. According to Ben Goldacre
147 patients with migraine took part, 74 had the NMT STARFlex device implanted, 73 had a fake operation with no device implanted, and 3 people in each group stopped having migraines. The NMT STARFlex device made no difference at all. This is not a statement of opinion, and there are no complex stats involved.
Goldacre’s article about the ensuing dustup and the 29 comments which follow make for very interesting reading, albeit discouraging if you want to have any faith in medical science.
Submitted by Paul Alper
Choosing the perfect March Madness bracket
“Trying for a Perfect Bracket? Insurers Will Take Those Odds”
by Erik Holm, The Wall Street Journal, March 23, 2012
Before the 2012 NCAA men’s basketball tournament, Fox Sports network ran an online contest, that offered a $1 million prize to anyone who could correctly pick all 63 March Madness games correctly. Fox also bought an insurance policy for the contest.
After just 16 games on the first day of March Madness ... fewer than 1% of the contestants still had perfect brackets .... By the time the field had been whittled to the Sweet 16 ... no one was left.
There are a number of companies offering to insure “all sorts of online competitions, wacky stunts, hole-in-one contests and even coupon giveaways.” While these companies do not generally disclose the cost of insurance, a representative of one company stated that his company charges about 2% of the prize value for a “perfect-bracket” competition and up to 15% for other competitions. In any case, these rates are said to be “still more than the odds might indicate.”
The website Book of Odds determined that picking the higher seed to win every matchup—generally the better bet for individual games—would result in odds of picking a perfect bracket of one in 35.4 billion. .... Other estimates have come up with better—but still minuscule—chances of success. Still, interviews with several experts who have arranged such contests yielded no one with a recollection of any contestant ever winning.
One contest-organizing company’s representative stated that none of the millions of entries they had received had come closer than 59 games out of 63 games.
A blogger commented[3], “I am surprised that Fox Sports does not self-insure since the premium appears to be overpriced by a factor of 700.”
Submitted by Margaret Cibes
New York City's teaching rankings
Here are three recent articles concerning New York City's controversial teacher rankings:
City teacher data reports are released
by Fernanda Santos and Sharon Otterman, New York Times, Schoolbook blog, 24 February 2012
After much legal wrangling, New York City has released its rankings of some 18,000 public school teachers in grades 4 through 8. The ranks are based on their students' performance on New York state's math and English exams over the five-year period ending with the 2009-10 school year. In response to concerns that the results might lead to criticism of individual teachers, officials sought to qualify the findings. We read
But citing both the wide margin of error — on average, a teacher’s math score could be 35 percentage points off, or 53 points on the English exam — as well as the limited sample size — some teachers are being judged on as few as 10 students — city education officials said their confidence in the data varied widely from case to case.
The rankings are value-added assessments. This means that students' actual performance on the exam is compared to how well they would statistically be expected to perform based on data which include their previous year's scores and various demographic variables such as race and economic status. As described in the article
If the students surpass the expectations, their teacher is ranked at the top of the scale — “above average” or “high” under different models used in New York City. If they fall short, the teacher receives a rating of “below average” or “low.” ...In New York City, a curve dictated that each year 50 percent of teachers were ranked “average,” 20 percent each “above average” and “below average,” and 5 percent each “high” and “low.”
The next article raises serious questions about the methodology, and questions whether the public will be able to appreciate its limitations.
Applying a precise label to a rough number
by Michael Winerip, New York Times, Schoolbook blog, 28 February 2012
Winerip sarcastically says how "delighted" he is that the scores have been released. He juxtaposes the cautions issued by school official, who said “We would never invite anyone — parents, reporters, principals, teachers — to draw a conclusion based on this score alone” with reaction in the press:
Within 24 hours The Daily News had published a front-page headline that read, “NYC’S Best and Worst Teachers.” And inside, on Page 4: “24 teachers stink, but 105 called great.”
This article also provides a more detailed description of the value-added calculations:
Using a complex mathematical formula, the department’s statisticians have calculated how much elementary and middle-school teachers’ students outpaced — or fell short of — expectations on annual standardized tests. They adjusted these calculations for 32 variables, including “whether a child was new to the city in pretest or post-test year” and “whether the child was retained in grade before pretest year.” This enabled them to assign each teacher a score of 1 to 100, representing how much value the teachers added to their students’ education.
In the next article, Winerip examines how the ratings went wrong at one particular school, P.S. 146 in Brooklyn.
Hard-working teachers, sabotaged when student test scores slip
by Michael Winerip, New York Times, 4 March 2012
According to the article, P.S. 146 has a reputation as a high-achieving school. In 2009, 96 percent of their fifth graders were proficient in English and 89 percent were proficient in math. Nevertheless, when the rankings were published, the school fared quite poorly. Several exceptionally qualified teachers received terrible scores. For example, Cora Sangree, whose resume includes training teachers at Columbia University's Teachers College, received an 11 in English and a 1 in math.
Winerip attributes such anomalies to the perverse nature of the value-added model. He explains
Though 89 percent of P.S. 146 fifth graders were rated proficient in math in 2009, the year before, as fourth graders, 97 percent were rated as proficient. This resulted in the worst thing that can happen to a teacher in America today: negative value was added.
The difference between 89 percent and 97 percent proficiency at P.S. 146 is the result of three children scoring a 2 out of 4 instead of a 3 out of 4.
Discussion
1. The value-added computations would seem to assume that the student groups are stable from year to year. What problems might there be here?
2. Look at the percentages given for each rating category ("low," "below average," "average" etc.). The article says these were dictated by a "curve". Do you suppose the value-added data were symmetric, or that this was a normal curve? What are the implications of such a scheme?
3. In the second article, Winerip comments on what seem like comically large margins of error.
Think of it this way: Mayor Michael R. Bloomberg is seeking re-election and gives his pollsters $1 million to figure out how he’s doing. The pollsters come back and say, “Mr. Mayor, somewhere between 13.5 percent and 66.5 percent of the electorate prefer you.”
This is an apparent reference to the 53 percent average margin of error stated in the first article for the English scores--but actually the width of a confidence interval would be twice the margin of error! But in any case, what does this suggest about the measurements?
Submitted by Bill Peterson, based on suggestions from Margaret Cibes and James Greenwood