Chance News 60

Quotations

"As a Usenet discussion grows longer, the probability of a comparison involving Nazis or Hitler approaches one."

Godwin's Law, as quoted at Wikipedia.

Submitted by Steve Simon

---

Chances are, the disparity between the [Commerce Department’s quarterly GDP report and the Labor Department’s monthly unemployment report] was mostly statistical noise. Those who read great meaning into either were deceiving themselves. It's a classic case of information overload making it harder to see the trends and patterns that matter. In other words, we might be better off paying less (or at least less frequent) attention to data. …. Most of us aren't professional forecasters. What should we make of the cacophony of monthly and weekly data? The obvious advice is to focus on trends and ignore the noise. But the most important economic moments come when trends reverse — when what appears to be noise is really a sign that the world has changed. Which is why, in these uncertain times, we jump whenever a new economic number comes out. Even one that will be revised in a month.

“Statistophobia: When Economic Indicators Aren’t Worth That Much”
by Justin Fox, TIME, February 1, 2010

Submitted by Margaret Cibes

Forsooth

"When the average age of the halftime act [at the Superbowl] is older than 47, the NFC team, the New Orleans Saints this year, has won nearly two-thirds of the time, and the games are about three times as likely to be blowouts."

For Sunday's halftime show, bet the over,
by Ben Austen, Wall Street Journal, 2 February 2010.

Submitted by Paul Alper

---

"Last year, nearly 5,000 teens

died in car crashes. Making it safer for a teen to be in a war zone than on a highway."

Allstate advertisement promoting a National Graduated Driver's License law.

Submitted by Bill Peterson

Does corporate support really subvert the data analysis

Corporate Backing for Research? Get Over It. John Tierney, The New York Times, January 25, 2010.

We've been warned many times to beware of corporate influences on research, and many reserach journals are now demanding more, in terms of disclosure and independent review, from researchers who have a conflict of interest. But John Tierney has argued that this effort gone too far.

Conflict-of-interest accusations have become the simplest strategy for avoiding a substantive debate. The growing obsession with following the money too often leads to nothing but cheap ad hominem attacks.

Mr. Tierney argues that this emphasis on money prevents thoughtful examination of all the motives associated with presentation of results

It is simpler to note a corporate connection than to analyze all the other factors that can bias researchers’ work: their background and ideology, their yearnings for publicity and prestige and power, the politics of their profession, the agendas of the public agencies and foundations and grant committees that finance so much scientific work.

Another emotion is at work, as well, snobbery.

Many scientists, journal editors and journalists see themselves as a sort of priestly class untainted by commerce, even when they work at institutions that regularly collect money from corporations in the form of research grants and advertising. We trust our judgments to be uncorrupted by lucre — and we would be appalled if, say, a national commission to study the publishing industry were composed only of people who had never made any money in the business. (How dare those amateurs tell us how to run our profession!) But we insist that others avoid even “the appearance of impropriety.”

Mr. Tierney cites a controversial requirement imposed by the Journal of the American Medical Association in 2005.

Citing “concerns about misleading reporting of industry-sponsored research,” the journal refused to publish such work unless there was at least one author with no ties to the industry who would formally vouch for the data.

This policy has been criticized by other journals.

That policy was called “manifestly unfair” by BMJ (formerly The British Medical Journal), which criticized JAMA for creating a “hierarchy of purity among authors.”

Submitted by Steve Simon.

Questions

1. Do you side with JAMA or BMJ on the policy of an independent author who can formally vouch for the data?

2. Should conflict of interest requirements be different for research articles involving subjective opinions, such as editorials, than for research involving objective approaches like clinical trials?

Snow-to-liquid ratios

Climatology of Snow-to-Liquid Ratio for the Contiguous United States”
by Martin A. Baxter, Charles E. Graves, and James T. Moore, Weather and Forecasting, October 2005

In this paper, two Saint Louis University professors report the results of a National Weather Service study of the ratio of snow to liquid, which concludes that the mean ratio for much of the country is 13, and not the “often-assumed value of 10.” The NWS studied climatology for 30 years. The study found “considerable spatial variation in the mean,” illustrated in lots of maps, tables, and histograms.

[A quantitative precipitation forecast (QPF)] represents the liquid equivalent expected to precipitate from [a weather] system. To convert this liquid equivalent to a snowfall amount, a snow-to-liquid-equivalent ratio (SLR) must be determined. An SLR value of 10 is often assumed as a mean value; however, this value may not be accurate for many locations and meteorological situations. Even if the forecaster has correctly forecasted the QPF, an error in the predicted SLR value may cause significant errors in forecasted snowfall amount.

The SLR of 10:1, as a rough approximation, dates from 1875. Subsequent similar estimates did “not account for geographic location or in-cloud microphysical processes.”

The goals of this paper are to present the climatological values of SLR for the contiguous United States and examine the typical variability using histograms of SLR for various NWS county warning areas (CWAs). [Sections of the paper describe] the datasets and methodology used to perform this research; [present] the 30-yr climatology of SLR for the contiguous United States; [detail] the frequency of observed SLR values through the use of histograms for selected NWS CWAs; [include] a brief discussion on how the climatology of SLR may be used operationally; and [summarize] the results and [present] suggestions for future research.

Submitted by Margaret Cibes at the suggestion of Jim Greenwood

An interesting problem

This hasn't hit the mainstream news yet but Bob Drake wrote us about an interesting problem. He wrote

Here is an example of e turning up unexpectedly. Select a random number between 0 and 1. Now select another and add it to the first, piling on random numbers. How many random numbers, on average, do you need to make the total greater than 1?

This appears in the notes of Derbyshire's book "Prime Obsession" pg 366 A proof of this can be found http://www.olimu.com/riemann/FAQs.htm here].

A version of the problem was posed in a 2004 Who's Counting column, entitled Imagining a Hit Thriller With Number 'e', where John Allen Paulos wrote:

Using a calculator, pick a random whole number between 1 and 1,000. (Say you pick 381.) Pick another random number (Say 191) and add it to the first (which, in this case, results in 572). Continue picking random numbers between 1 and 1,000 and adding them to the sum of the previously picked random numbers. Stop only when the sum exceeds 1,000. (If the third number were 613, for example, the sum would exceed 1,000 after three picks.)

How many random numbers, on average, will you need to pick?

We mentioned this to Charles Grinstead who wrote:

It appears in Feller, vol. 2. But more interesting than that problem is the following generalization: Pick a positive real number M, and play the same game as before, i.e. stop when the sum first equals or exceeds M. Let f(M) denote the average number of summands in this process (so the game that he was looking at corresponds to M = 1, and he saw that it is known that f(1) = e). Clearly, since the average size of the summands is 1/2, f(M) should be about 2M, or perhaps slightly greater than 2M. For example, when M = 1, f(M) is slightly greater than 2. It can be shown that as M goes to infinity, f(M) is asymptotic to 2M + 2/3.

Submitted by Laurie Snell

Girls and math study

“Female teachers’ math anxiety affects girls’ math achievement”
“Appendices: Questionnaires”
“Supporting Information: Statistics”
by Sian L. Beilock, Elizabeth A. Gunderson, Gerardo Ramirez, and Susan C. Levine, Proceedings of the National Academy of Sciences, January 25, 2010

Four University of Chicago psychologists studied math anxiety and its effect on the math achievement of 65 girls and 52 boys taught by 17 female elementary-school teachers. Extensive details about methodology and statistics are provided in the paper, its two appendices, and the supporting information.

The researchers summarized their conclusions in the Abstract:

…. There was no relation between a teacher’s math anxiety and her students’ math achievement at the beginning of the school year. By the school year’s end, however, the more anxious teachers were about math, the more likely girls (but not boys) were to endorse the commonly held stereotype that “boys are good at math, and girls are good at reading” and the lower these girls’ math achievement.

At the end of the paper they state:

… [W]e did not find gender differences in math achievement at either the beginning ... or end ... of the school year. However, … by the school year’s end, girls who confirmed traditional gender ability roles performed worse than girls who did not and worse than boys more generally. We show that these differences are related to the anxiety these girls’ teachers have about math. .... [I]t is an open question as to whether there would be a relation between teacher math anxiety and student math achievement if we had focused on male instead of female teachers.

Submitted by Margaret Cibes at the suggestion of Cathy Schmidt

Political illiteracy

Lost in translation
New York Times, 29 January 2010
Charles M. Blow

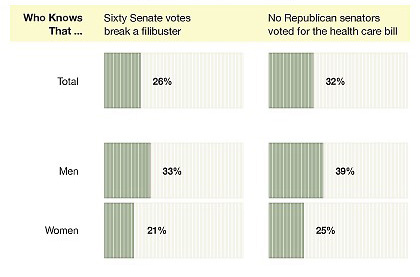
Chance News often features examples of innumeracy or statistical illiteracy, but what about political illiteracy? Congress has spent a year debating health care reform, and the stalled legislation was widely discussed in coverage of President Obama's State of the Union address. Nevertheless, in above article we read that: "According to a survey released this week by the Pew Research Center for the People and the Press, only 1 person in 4 knew that 60 votes are needed in the Senate to break a filibuster and only 1 in 3 knew that no Senate Republicans voted for the health care bill."

The above reproduces a portion of an accompanying graphic entitled Widespread Political Illiteracy, which breaks out responses further based on age, education, political affiliation, etc. The results are not encouraging.

The article provides a link to an online quiz at the Pew Research Center website, where readers can test their own knowledge. Of the dozen questions there, the filibuster item had the worst score in the survey.

Blow suggests that a possible source of all the confusion may be people's choice of news outlets. He cites another recent poll which found that Fox News was the most trusted network news in the country, with 49% of respondents expressing trust. The ABC, NBC and CBS networks all got less than 40%. The full results from Public Policy Polling organization are available here. Political affiliation appeared to be a key factor. Fox was trusted by 74% of Republican respondents but only 30% of Democrats. By contrast, the other three networks were all trusted by a majority of Democrats but less than 20% of Republicans. According to Dean Debnan, President of Public Policy Polling,

A generation ago you would have expected Americans to place their trust in the most neutral and unbiased conveyors of news. But the media landscape has really changed and now they’re turning more toward the outlets that tell them what they want to hear.

Submitted by Paul Alper

Baby Einstein wants data

‘Baby Einstein’ Founder Goes to Court. Tamar Lewin, The New York Times, January 12, 2010.

"Baby Einstein" is a series of videos targeted at children from 3 months to 3 years. They expose children to music and images that are intended to be educational. These videos were popularized in part by the so-called Mozart effect.

The use of such videos had been discouraged by the American Academy of Pediatrics, but a series of peer-reviewed articles showed that exposure to these videos could actually do more harm than good.

So the owner of the Einstein video series did what any red-blooded American would do. He sued the researchers.

A co-founder of the company that created the “Baby Einstein” videos has asked a judge to order the University of Washington to release records relating to two studies that linked television viewing by young children to attention problems and delayed language development.

What would he do with all that data?

“All we’re asking for is the basis for what the university has represented to be groundbreaking research,” the co-founder, William Clark, said in a statement Monday. “Given that other research studies have not shown the same outcomes, we would like the raw data and analytical methods from the Washington studies so we can audit their methodology, and perhaps duplicate the studies, to see if the outcomes are the same."

Asking for the raw data to conduct a re-analysis is a commonly used tactic among commercial sources harmed by unfavorable research published in the peer-reviewed literature. Here is a nice historical summary of these efforts.

Submitted by Steve Simon

Questions

1. Does a commercial interest have an inherent right to review data that harms the sales of its product?

2. Should the data from taxpayer subsidized research be made available to the general public?

3. What harms might a researcher suffer if he/she was forced to disclose raw data associated with a study?

Million, billion...whatever

Milo Schield sent the following article to the ASA Statistical Education eGroup.

But who's counting?
Los Angeles Times, 31 January 2010
Doug Smith

This op/ed piece poses the following question: "The million-billion mistake is among the most common in journalism. But why?" Smith's research identified 23 instances of this mix-up in the Times over the last three years, most often in stories about money. For example, the paper reported that California spent $59.7 million on education in 2008-09, when the correct figure was $59.7 billion.

Lynn Arthur Steen, emeritus professor of mathematics at St. Olaf College, is quoted as explaining

Generally people do not have sufficient experience with large numbers to have any intuitive sense of their size. They have no "anchor" to distinguish a million from a billion the way they might "feel" the difference between $10 and $10,000. So mistakes easily slip by unnoticed.

Milo teaches at Augsburg College in Minneapolis, where he has developed a course in quantitative journalism. The article quotes his recommendation:

Newspapers should always break large numbers down into rates that make sense, he said. Rather than simply talking about California's $59-billion education budget, newspapers should break that out as $4,900 per household (ouch!), not the $4.90 it would be if the figure were in millions.

Submitted by Bill Peterson

Surgical risk calculators

“New Ways to Calculate the Risks of Surgery”
by Laura Lanro, The Wall Street Journal, February 2, 2010

This article discusses a “new risk calculator that handicaps an individual patient's chances of surgical complications based on personal medical history and physical condition ... [developed using] data from more than one million patient records gathered as part of the … National Surgical Quality Improvement Program ….” While cardiac surgeons have had a risk calculator tool for a while, it is only recently that other surgeons have had a similar tool.

A website, “euroScore”, provides access to two calculators of cardiac-surgery risk – a “simple additive score” and a “logistic” score. The former is an automatically calculated score based on the variables Age (years), Gender (Male/Female), LV function (Poor/Moderate/Good), and 14 medical conditions (Yes/No). The latter is a hand calculation explained at “How to calculate the logistic EuroSCORE”. These scores are based on 97 risk factors in nearly 20,000 “consecutive patients from 128 hospitals in eight European countries"; see “How was it developed”. Physicians are “invited to try out both models and to use the one most suitable to [their] practice.”

Outside of the cardiac-surgery specialty, colorectal-surgery risk calculations are based on 15 variables and data from approximately 30,000 surgery patients at 182 hospitals for the period 2006-2007.

One doctor has stated:

[The calculator] not only helps assess whether the patient is a good candidate for surgery, but also helps him make sure patients understand what they are getting into – the process known as "informed consent."

Another physician stated:

Telling a patient there is a risk of dying from a cancer surgery is not an easy conversation to have. …. The calculator is a tool you need to use in a judicious way, so as not to scare the patients, but to make them feel more comfortable that you are being honest and open with them.

Discussion

1. Besides the patient's pre-surgery medical conditions, what other aspects of physician or hospital care might affect his/her risk of complications from cardiac surgery?

2. Using the standard calculator for cardiac-surgery risk on females age 1, 25, 50, 75, or 100 years, the risk ranges from 0 in the best cases to 34, 34, 34, 38, or 43, respectively, in the worst cases. Does anything about these results strike you as surprising? How would you interpret a particular risk, say 20, on this scale?

3. Using the logistic calculator for cardiac-surgery risk on females age 1, 25, 50, 75, or 100 years, the risk ranges from 0 in the best cases to 99.91%, 99.91%, 99.91%, 99.97%, or 99.99%, respectively, in the worst cases. Which scale - standard or logistic - has more meaning for you? What meaning? Why?

4. Would a risk number help you to make a more informed decision about cardiac surgery? What other statistic(s) might be helpful to specific patient with respect to a doctor or hospital?

Submitted by Margaret Cibes