Chance News 100: Difference between revisions
| Line 157: | Line 157: | ||
The strategy is to continue if this exceeds W. Solving the inequality gives the simple condition ''R'' > ''W''. | The strategy is to continue if this exceeds W. Solving the inequality gives the simple condition ''R'' > ''W''. | ||
The article describes two more involved versions of the puzzle, with an interactive feature for each scenario so that you can develop a feel for the play. A colleague of Prof. Tijms has provided a [http://personal.vu.nl/a.a.n.ridder/java/dpp.html full simulation | The article describes two more involved versions of the puzzle, with an interactive feature for each scenario so that you can develop a feel for the play. A colleague of Prof. Tijms has provided a [http://personal.vu.nl/a.a.n.ridder/java/dpp.html full online simulation] for the first version. | ||
Submitted by Bill Peterson | Submitted by Bill Peterson | ||
Revision as of 22:14, 1 August 2014
Quotations
"Steve Ziliak, a critic of RCTs [randomised controlled trials], complains about one conducted in China in which some visually-impaired children were given glasses while others received nothing. The case against the trial is that we no more need a randomised trial of spectacles than we need a randomised trial of the parachute."
Submitted by Paul Alper
“Chance is commonly viewed as a self-correcting process in which a deviation in one direction induces a deviation in the opposite direction to restore the equilibrium. In fact, deviations are not 'corrected' as a chance process unfolds, they are merely diluted.”
Submitted by Bill Peterson
“If the statistics courses are not providing basic statistical intuition, it is not necessarily because they failed to cover the material, but perhaps just the opposite. That is, by covering so many topics, they may yield a poor signal to noise ratio when it comes to the basics.” [p. 269, author’s emphasis]
“I refer to … ‘consumer stochastics’ …. This differs from the overall field of statistics only in its target audience. Whereas statistics has aided scientists … in almost every discipline …, consumer stochastics is aimed at non-scientists …, who face uncertainty on a regular basis, that is, most professionals.” [p. 270]
Statistics and Public Policy, 1997
Submitted by Margaret Cibes
"The point is that just because one event sometimes follows another it does not follow that the following event is caused by that by which it is preceded. That this fallacy does, in fact, regularly get past your average journalist entitles it to a name: the post hoc, passed back fallacy."
"If only they could invent a drug that would cure journalistic impotence and permit hacks to have some meaningful intercourse with science. Now there would be a medical breakthrough."
Cambridge University Press, 2003, p. 109
Submitted by Margaret Cibes
Forsooth
One sentence too many?
“At issue was how highly correlated the prices of various subprime mortgage bonds inside a CDO might be. Possible answers ranged from 0 percent (their prices had nothing to do with each other) to 100 percent (their prices moved in lockstep with each other). Moody’s and Standard & Poor’s judged the pools of triple-B-rated bonds to have a correlation of around 30 percent, which did not mean anything like what it sounds. It does not mean, for example, that if one goes bad, there is a 30 percent chance that the others will go bad too. It means that if one bond goes bad, the others experience very little decline at all.”
Submitted by Margaret Cibes
“When confronted with data from the Centers for Disease Control that seemed to provide scientific refutation of her claims [that vaccines caused autism, Jenny] McCarthy responded, ‘My science is named Evan [her son] and he’s at home. That’s my science.’ …. She is fond of saying that she acquired her knowledge of vaccinations and their risks at ‘the University of Google.’” [p. 79]
“[Dr. Andrew] Weil doesn’t buy into the idea that clinical evidence is more valuable than intuition. Like most practitioners of alternative medicine, he regards the scientific preoccupation with controlled studies, verifiable proof, and comparative analysis as petty and one dimensional.” [p. 257]
"[T]he National Center for Complementary and Alternative Medicine is the brainchild of Iowa senator Tom Harkin, who was inspired by his conviction that taking bee pollen cured his allergies …. There is no evidence that bee pollen cures allergies or lessens their symptoms. ….
In Senate testimony in March 2009, Harkin said he was disappointed in the work of the center because it had disproved too many alternative therapies. ‘One of the purposes of this center was to investigate and validate alternative approaches. Quite frankly, I must say publicly that it has fallen short,’ Harken said.” [pp. 174, 180]
“I don’t have either APOE4 allele, which is a great relief. ‘You dodged a bullet,’ my extremely wise physician said when I told him the news. ‘But don’t forget they might be coming out of a machine gun.” [p. 220]
Submitted by Margaret Cibes
"Another example of that interest was data from TiVo showing that although four of the top five streamed games of the tournament in homes with TiVo DVRs involved the United States team, six of the 10 most-streamed games involved teams from other countries." [One must bear in mind that the US played in exactly four games in the World Cup!]
Submitted by David Czerwinski
The Guardian reported that the British intelligence agency GCHQ secretly collected images of Yahoo webcam chats in bulk. The program was called Optic Nerve, according to documents revealed by Edward Snowden, and many of the images contain sexually explicit ("undesirable") material. The Guardian article discusses Yahoo's response to this report, the legality of the Optic Nerve and other GCHQ efforts, how GCHQ handled explicit images, and how the agency attempted to estimate the proportion of Yahoo accounts with explicit images. The article contains this paragraph from one of the GCHQ documents:
- "A survey was conducted, taking a single image from each of 323 user ids. 23 (7.1%) of those images contained undesirable nudity. From this we can infer that the true proportion of undesirable images in Yahoo webcam is 7.1% ± 3.7% with confidence 95%."
However, the calculation seems to have been made at the 99% confidence level. For 95% confidence, the margin of error would be smaller, only ±2.8%.
Submitted by Alan Shuchat
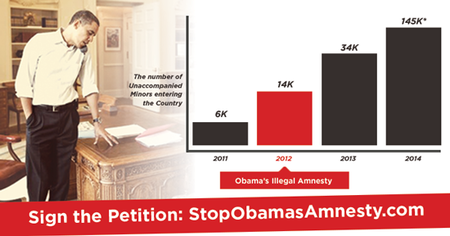
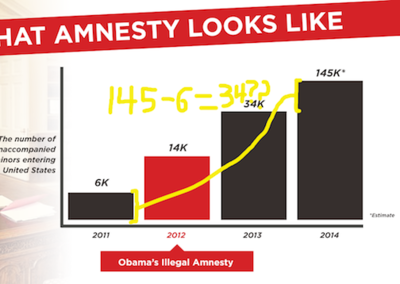
Yglesias adds: "It's not clear exactly why Cruz's team made the chart this way. Perhaps they thought that showing a huge surge happening with a one-year delay would make the argument less convincing. Perhaps they just don't know how to make charts."
Submitted by Priscilla Bremser
The Oxford comma: A pressing issue?
Elitist, superfluous, Or popular? We polled Americans on the Oxford comma
By Walt Hickey, FiveThirtyEight, 17June 2014
A grammatical point of controversy: should you use a comma before the "and" in a list of more than two items? As reported in the article:
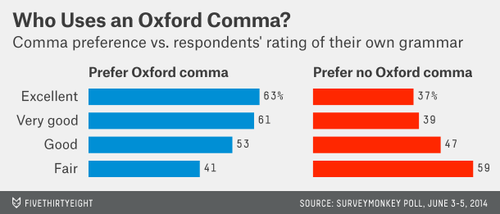
We asked respondents which sentence was, in their opinion, more grammatically correct: “It’s important for a person to be honest, kind and loyal.” Or: “It’s important for a person to be honest, kind, and loyal.” The latter has an Oxford comma, the former none.
Among 1129 Americans responding, the Oxford comma was preferred, 57% to 43%. Interestingly, those in favor tended to have a higher opinion of their own grammatical skills, as shown in the accompanying graph
Lest you get the impression that this is simply a matter of taste, see The best shots fired in the Oxford comma wars. Among the amusing examples there:
Pro: "She took a photograph of her parents, the president, and the vice president."
This example from the Chicago Manual of Style shows how the comma is necessary for clarity. Without it, she is taking a picture of two people, her mother and father, who are the president and vice president. With it, she is taking a picture of four people.
Con: "Those at the ceremony were the commodore, the fleet captain, the donor of the cup, Mr. Smith, and Mr. Jones."
This example from the 1934 style book of the New York Herald Tribune shows how a comma before "and" can result in a lack of clarity. With the comma, it reads as if Mr. Smith was the donor of the cup, which he was not.
Submitted by Paul Alper
Interpreting climate change probabilities
Bob Griffin sent a link to the following
- The interpretation of IPCC probabilistic statements around the world
- by David V. Budescu, et al, Nature Climate Change, 20 April 2014
which he describes as "an intriguing look at how folks in different cultures around the world interpret the verbal statements of uncertainty that the Intergovernmental Panel on Climate Change uses. They found that an alternative presentation format (verbal terms with numerical ranges) improves the correspondence between the IPCC guidelines and public interpretations. The alternative presentation format also produces more stable results across cultures."
On the Nature site, only the abstract is available to non subscribers, but you can read more about the study design in this Fordham University press release. As described there:
The study asked over 11,000 volunteers in 24 countries (and in 17 different languages) to provide their interpretations of a the intended meaning and possible range of 8 sentences form the IPCC report that included the various phrases. For example, one sentence read: “It is very likely that hot extremes, heat waves, and heavy precipitation events will continue to become more frequent.” Only a small minority of the participants interpreted the probability of that statement consistent with IPCC guidelines (over 90 percent), and the vast majority interpreted the term to convey a probability in around 70 percent.
A similar effect was observed with other phrases: When verbal descriptions were given without numerical ranges, readers tended to interpret the probabilities as being closer to 50 percent than intended by the guidelines.
The Wikipedia entry on Words of estimative probability provides some perspective on this, illustrating that different verbal descriptions are used in different fields. The phrase "words of estimative probability" (WEP) is described as originating in the intelligence community. (The lack of preparation prior to the 9/11 attacks is cited as a famous failure in risk communication.) But as described here, a different set of phrases are used in the medical community in the context of informed patient decision making.
Summer reading
Past, Present, and Future of Statistical Science, Chapman and Hall/CRC, 2014
This free pdf download is the result of a project of the Committee of Presidents of Statistical Societies (COPSS) to assemble from almost 50 statisticians their reminiscences, personal reflections, and perspectives on the discipline and profession, as well as advice for the next generation. The contributions are relatively short, very good reads.
Submitted by Margaret Cibes
Probability of precipitation
John Emerson sent a link to the following:
Pop quiz: 20 percent chance of rain. Do you need an umbrella?
“All Things Considered,” NPR, 22 July 2014
This is part of a weeklong series on NPR, called Risk and reason, that explores people's understanding of chance. Noting that weather forecasts represent an almost daily encounter with probability statements, NPR interviewers set out to explore what the person in the street understands by the phrase “20 percent chance of rain.” You can listen to some responses in the audio segment (about 7.5 minutes) provided at the above link, or read the synopsis there. Not surprisingly, there a variety of answers, most not very scientific.
NPR listeners pointed out the the segment itself failed to produce a succinct answer, so NPR produced a short followup story the next day Confusion with a chance of clarity: Your weather questions, answered (23 July 2014). Included there were descriptions from two meteorology experts. Eli Jacks, of the National Weather Service said:
There's a 20 percent chance that at least one-hundreth of an inch of rain — and we call that measurable amounts of rain — will fall at any specific point in a forecast area.
Jason Samenow, of the Capital Weather Gang at the Washington Post offered this:
It simply means for any locations for which the 20 percent chance of rain applies, measurable rain (more than a trace) would be expected to fall in two of every 10 weather situations like it.
More detailed discussion can be found at this FAQ page from NOAA, where we read
Mathematically, PoP [probability of precipitation] is defined as follows:
- PoP = C x A where "C" = the confidence that precipitation will occur somewhere in the forecast area, and where "A" = the percent of the area that will receive measureable precipitation, if it occurs at all.
Discussion
Are the two weather experts quoted above saying the same thing? Do their descriptions square with the mathematical definition?
The devil’s penny puzzle
Henk Tijms and the devil’s penny
by Gary Antonick, Numberplay blog, New York Times, 3 March 2014
The following puzzle was created by emeritus Professor Henk Tijms of Vrije University in Amsterdam.
Ten boxes are placed in front of you and money is put into each box: two dollars, for example, goes in one of the boxes; five dollars in another box, and so on. You’re able to see each of the values. An eleventh box containing a Devil’s penny is added to the mix. The boxes are then closed and rearranged so that you can’t tell which box contains which amount of money — or if a particular box contains the dreaded Devil’s penny. You may then open up, one by one, as many boxes as you’d like and keep the money inside — but if you open the box with the Devil’s penny you lose everything. When should you stop?
The article notes that the solution has an appealingly simple form: To maximize the expected value of your winnings, you should stop when your accumulated fortune is greater than or equal to the amount of money remaining in unopened boxes (of course, if you get the Devil’s penny you are forced to stop with nothing). Prof. Tijms notes that a formal proof of optimality would rely on the Bellman equation from dynamic programming; nevertheless, he was pleased to find that several readers’ comments revealed key insights. You may want to look through these at the link above.
Indeed, the article itself contains the seeds of a solution by backward induction (or “value iteration”). Consider the number of boxes remaining unopened. If there is only one, it must contain the devil’s penny, so you stop. If there are two, then one is the devil’s penny and one has money. Since you are equally likely to get either by continuing, it makes sense (in expected value terms) to stop unless there is more money remaining than you already have won.
One of the interesting insights is that the optimal strategy considers only the total money available, not how is distributed across the boxes. To see this, we borrow notation from one of the commenters (“Matt”). If n boxes remain, you have won W dollars so far, and R dollars remain, then the conditional expected value of a box, given that it is not the devil’s penny, is given by R/(n-1), regardless of now the R dollars are distributed. Your expected fortune by continuing is therefore: [W + R /(n-1)] * [(n-1)/n] + (0) *(1/n).
The strategy is to continue if this exceeds W. Solving the inequality gives the simple condition R > W.
The article describes two more involved versions of the puzzle, with an interactive feature for each scenario so that you can develop a feel for the play. A colleague of Prof. Tijms has provided a full online simulation for the first version.
Submitted by Bill Peterson