Sandbox: Difference between revisions
| Line 18: | Line 18: | ||
<br><br> | <br><br> | ||
Your challenge is to design a game, using only a fair coin, that you have a 1/3 chance of winning. | Your challenge is to design a game, using only a fair coin, that you have a 1/3 chance of winning. | ||
<blockquote> | </blockquote> | ||
Continues "And here is my recipe for getting the most out of this problem: if you can solve it, do not stop with one answer. Rather, see how many answers you can come up with. I’ve posed this problem to many people, and I continue to hear novel solutions." | Continues "And here is my recipe for getting the most out of this problem: if you can solve it, do not stop with one answer. Rather, see how many answers you can come up with. I’ve posed this problem to many people, and I continue to hear novel solutions." | ||
Revision as of 02:06, 26 March 2014
March bracket madness
Mathematicians are hoping their calculations add up to the perfect bracket
by Mary Pilon, New York Times, 15 March 2014
In N.C.A.A. tournament bracket, mathematician outdoes Matildas
by Joe Drape, New York Times, 24 March 2014
Two alcohol graphics
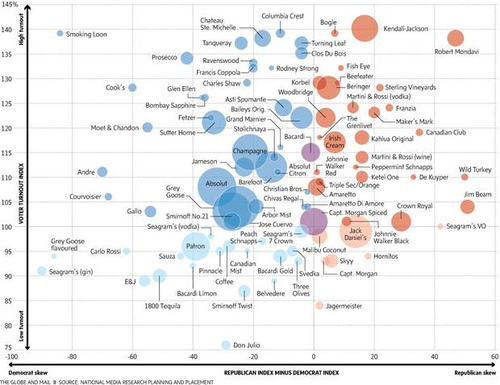
Tell me what you drink, and I’ll tell you how you’ll vote
by Beppi Crosariol, The Globe and Mail, 14 January 2014
Includes the following chart, entitled What Americans drink and how they vote
A pair of probability puzzles
Consider this simple game: flip a fair coin twice. You win if you get two heads, and lose otherwise. It’s not hard to calculate that the chances of winning are 1/4.
Your challenge is to design a game, using only a fair coin, that you have a 1/3 chance of winning.
Continues "And here is my recipe for getting the most out of this problem: if you can solve it, do not stop with one answer. Rather, see how many answers you can come up with. I’ve posed this problem to many people, and I continue to hear novel solutions."
A large urn
by Gary Antonik, Numberplay blog, New York Times, 24 March 2014
There are 600 black marbles and 400 white marbles mixed well in a large urn. You draw marbles one by one at random without replacement until you take out all the marbles of one of the colors. What is the probability that at least one white marble will be left in the urn?
Bonus: On average, how many marbles will be left in the urn?
Submitted by Bill Peterson