Sandbox: Difference between revisions

From ChanceWiki
Jump to navigation Jump to search
 
Line 1: Line 1:
==The Bulgarian Toto 6 of 42 lottery==


The  Bulgarian Toto 6 of 42 lottery was the subject of an investigation after the
[http://www.novinite.com/view_news.php?id=107914] same set of six numbers {4, 15, 23, 24, 35, 42} was drawn in two successive lotteries on September 6 and September 10, 2009. The article cites a mathematician as stating that the probability of picking the same six numbers twice in a row is 4,200,000:1.  We wondered how he arrived at this number.  What is the probability that a specified set of six numbers will repeat consecutively?


There are <math>{42 \choose 6} = 5245786</math> different sets of six numbers and the probability that a SPECIFIED set will occur in the next two consecutive draws is <math>1/5245786^2</math>.  Because the sets involve disjoint events, the probability that SOME set will occur in the next two consecutive draws is  <math>5245786 \times 1/5245786^2 = 1/5245786</math>. 
==Forsooth==


But now, suppose the lottery has been running continuously for <math>m</math> draws and we ask what the chance is that during this period there were consecutive draws of the same set.  As before, first consider a fixed set of six numbers.
==Quotations==
“We know that people tend to overestimate the frequency of well-publicized, spectacular
events compared with more commonplace ones; this is a well-understood phenomenon in
the literature of risk assessment and leads to the truism that when statistics plays folklore,
folklore always wins in a rout.”
<div align=right>-- Donald Kennedy (former president of Stanford University), ''Academic Duty'', Harvard University Press, 1997, p.17</div>


There are <math>m-1</math> opportunities for this set to be drawn twice in succession (beginning with the second drawing). The probability that this will happen is then the probability of the union <math>P(A) = P(\cup_i A_i A_{i+1}) </math> where <math>A_i</math> is the event that this set of numbers is drawn on the ith draw.
----


Bonferroni's inequality gives the upper bound <math>P(A) \le \sum_i P(A_i A_{i+1})</math> while Hunter's inequality gives the lower bound <math>P(A) \ge \sum_i P(A_i A_{i+1}) - \sum_i P(A_i A_{i+1}A_{i+2}).</math>
"Using scientific language and measurement doesn’t prevent a researcher from conducting flawed experiments and drawing wrong conclusions — especially when they confirm preconceptions."


We assume (!) that the events <math>A_i</math> are independent and identically distributed with probability <math>p = 1/5245786</math> leading to <math>(m-1) p^2  - (m-2) p^3 \le P(A) \le (m-1) p^2</math>.  Since
<div align=right>-- Blaise Agüera y Arcas, Margaret Mitchell and Alexander Todoorov, quoted in: The racist history behind facial recognition, ''New York Times'', 10 July 2019</div>
<math>p</math> is very small the <math>p^3</math> term can be ignored
giving <math>P(A) \approx (m-1)/5245786^2.</math>


It appears that the draws are held twice per week so for one year <math>m = 104</math> giving the probability <math>3.74 \times 10^{-12}</math> that a specified set of numbers will be drawn twice in succession.  According to a spokeswoman the lottery has been taking place for 52 years
==In progress==
[http://www.canada.com/Bulgaria+identical+lottery+draw+just+coincidence/2003980/story.html?id=2003980x].
[https://www.nytimes.com/2018/11/07/magazine/placebo-effect-medicine.html What if the Placebo Effect Isn’t a Trick?]<br>
Using <math>m = 104 \times 52 = 5408</math>, the probability that a specified set of numbers will be drawn twice in succession over this period is <math>1.89 \times 10^{-10}</math>, still very small.
by Gary Greenberg, ''New York Times Magazine'', 7 November 2018


But now let's ask the question, not for a fixed set of numbers but for some set of numbers. After all, in discussing this coincidence the the repeated set arises by chance alone and is not specified in advance.
[https://www.nytimes.com/2019/07/17/opinion/pretrial-ai.html The Problems With Risk Assessment Tools]<br>
by Chelsea Barabas, Karthik Dinakar and Colin Doyle, ''New York Times'', 17 July 2019


In <math>m</math> drawings what is the probability that SOME set of six numbers will be repeated in consecutive draws.
==Hurricane Maria deaths==
Laura Kapitula sent the following to the Isolated Statisticians e-mail list:


There are 5245786 possible sets of numbers that could be repeated. Enumerate the sets by integers
:[Why counting casualties after a hurricane is so hard]<br>
<math>1 \le k ≤ \le 5245786</math> with <math>E_k</math> the event that set <math>k</math> repeats consecutively sometime during
:by Jo Craven McGinty, Wall Street Journal, 7 September 2018
these <math>m</math> drawings. The probability of the union <math>P(\cup E_k)</math> is needed. Each of the 5245786 events
<math>E_k</math> has probability <math>(m-1)/ 5245786^2</math> and if they were independent we could evaluate the probability using complements as
<math>P(\cup E_k) = 1 - (1- (m-1)/5245786^2)^{5245786} \approx 1 - e^{-(m-1)/5245786}</math>. However, they are dependent, but as long as <math>m</math> is small relative to 5245786, Bonferroni's and Hunter's bounds can once again be used to estimate
<math>P(\cup E_k) \approx (m-1)/5245786.</math> For <math>m = 5408</math> this is 0.0010302. (Note that assuming independence gives 0.0010307)


This probability relates to one lottery. Suppose we consider all lotteries worldwise and ask for the probability that in some lottery, somewhere, some set of numbers will be repeated consecutively. All lotteries are variant of Toto with different numbers involved. Each lottery will have had its own cumulative number of drawings. In order to gauge the magnitude of the probability wanted, assume that there are <math>x</math> lotteries, each one sharing the same numerical characteristics as the Bulgarian one.
The article is subtitled: Indirect deaths—such as those caused by gaps in medication—can occur months after a storm, complicating tallies
Laura noted that
:[https://www.washingtonpost.com/news/fact-checker/wp/2018/06/02/did-4645-people-die-in-hurricane-maria-nope/?utm_term=.0a5e6e48bf11 Did 4,645 people die in Hurricane Maria? Nope.]<br>
:by Glenn Kessler, ''Washington Post'', 1 June 2018


This time we can use independence. The probability that some set will be repeated is 1 minus the probability that in no lottery is a set of numbers selected on two consecutive drawings
The source of the 4645 figure is a [https://www.nejm.org/doi/full/10.1056/NEJMsa1803972 NEJM article].  Point estimate, the 95% confidence interval ran from 793 to 8498.
<math>= 1 - (1 - (m -1)/5245786)^x</math>. For <math>x = 50</math> this is 0.0503 while for <math>x = 100</math> the probability is 0.0980. (An approximation to one significant digit for this range of values of interest is <math>x(m-1)/5245786.</math>)


For a different problem that discusses "very big numbers" see the article about  double lottery winners [http://www.nytimes.com/1990/02/27/science/1-in-a-trillion-coincidence-you-say-not-really-experts-find.html?pagewanted=all].
President Trump has asserted that the actual number is
[https://twitter.com/realDonaldTrump/status/1040217897703026689 6 to 18].
The ''Post'' article notes that Puerto Rican official had asked researchers at George Washington University to do an estimate of the death toll.  That work is not complete.
[https://prstudy.publichealth.gwu.edu/ George Washington University study]


Questions.
:[https://fivethirtyeight.com/features/we-still-dont-know-how-many-people-died-because-of-katrina/?ex_cid=538twitter We sttill don’t know how many people died because of Katrina]<br>
:by Carl Bialik, FiveThirtyEight, 26 August 2015


1. Instead of Hunter's lower bound, what would the second Bonferroni bound give?
----
[https://www.nytimes.com/2018/09/11/climate/hurricane-evacuation-path-forecasts.html These 3 Hurricane Misconceptions Can Be Dangerous. Scientists Want to Clear Them Up.]<br>
[https://journals.ametsoc.org/doi/abs/10.1175/BAMS-88-5-651 Misinterpretations of the “Cone of Uncertainty” in Florida during the 2004 Hurricane Season]<br>
[https://www.nhc.noaa.gov/aboutcone.shtml Definition of the NHC Track Forecast Cone]
----
[https://www.popsci.com/moderate-drinking-benefits-risks Remember when a glass of wine a day was good for you? Here's why that changed.]
''Popular Science'', 10 September 2018
----
[https://www.economist.com/united-states/2018/08/30/googling-the-news Googling the news]<br>
''Economist'', 1 September 2018


2. How many years would the Bulgarian lottery need to be running in order to have the same probability that some set of numbers will appear three times in succession?
[https://www.cnbc.com/2018/09/17/google-tests-changes-to-its-search-algorithm-how-search-works.html We sat in on an internal Google meeting where they talked about changing the search algorithm — here's what we learned]
----
[http://www.wyso.org/post/stats-stories-reading-writing-and-risk-literacy Reading , Writing and Risk Literacy]


3. Instead of demanding that the same set of numbers appear twice in succession, what is the probability that some set of numbers will repeat during <math>m</math> drawings (This is simpler and is the famous birthday problem).
[http://www.riskliteracy.org/]
-----
[https://twitter.com/i/moments/1025000711539572737?cn=ZmxleGlibGVfcmVjc18y&refsrc=email Today is the deadliest day of the year for car wrecks in the U.S.]


4.  The second application of Hunter's bound requires estimating <math>\sum  P( E_{k} E_{k+1} )</math> which involves terms of the form <math>P(A_i A_{i+1} B_j B_{j+1} )</math> where <math>A_i</math> is the event that the set <math>k</math> occurs on draw <math>i</math> and <math>B_j</math> is the event
==Some math doodles==
that the
<math>P \left({A_1 \cup A_2}\right) = P\left({A_1}\right) + P\left({A_2}\right) -P \left({A_1 \cap A_2}\right)</math>
set <math>k+1</math> occurs on draw <math>j</math>. Each of these terms has probability
<math>1/5245786^4</math>. Count the number of terms to validate the claim that <math>P(\cup_k E_k) \approx (m-1)/5245786</math>.


Submitted by Fred Hoppe
<math>P(E)  = {n \choose k} p^k (1-p)^{ n-k}</math>
 
<math>\hat{p}(H|H)</math>
 
<math>\hat{p}(H|HH)</math>
 
==Accidental insights==
 
My collective understanding of Power Laws would fit beneath the shallow end of the long tail. Curiosity, however, easily fills the fat end.  I long have been intrigued by the concept and the surprisingly common appearance of power laws in varied natural, social and organizational dynamics.  But, am I just seeing a statistical novelty or is there meaning and utility in Power Law relationships? Here’s a case in point.
 
While carrying a pair of 10 lb. hand weights one, by chance, slipped from my grasp and fell onto a piece of ceramic tile I had left on the carpeted floor. The fractured tile was inconsequential, meant for the trash.
<center>[[File:BrokenTile.jpg | 400px]]</center>
As I stared, slightly annoyed, at the mess, a favorite maxim of the Greek philosopher, Epictetus, came to mind: “On the occasion of every accident that befalls you, turn to yourself and ask what power you have to put it to use.”  Could this array of large and small polygons form a Power Law? With curiosity piqued, I collected all the fragments and measured the area of each piece.
 
<center>
{| class="wikitable"
|-
! Piece !! Sq. Inches !! % of Total
|-
| 1 || 43.25 || 31.9%
|-
| 2 || 35.25 ||26.0%
|-
|  3 || 23.25 || 17.2%
|-
| 4 || 14.10 || 10.4%
|-
| 5 || 7.10 || 5.2%
|-
| 6 || 4.70 || 3.5%
|-
| 7 || 3.60 || 2.7%
|-
| 8 || 3.03 || 2.2%
|-
| 9 || 0.66 || 0.5%
|-
| 10 || 0.61 || 0.5%
|}
</center>
<center>[[File:Montante_plot1.png | 500px]]</center>
The data and plot look like a Power Law distribution. The first plot is an exponential fit of percent total area. The second plot is same data on a log normal format. Clue: Ok, data fits a straight line.  I found myself again in the shallow end of the knowledge curve. Does the data reflect a Power Law or something else, and if it does what does it reflect?  What insights can I gain from this accident? Favorite maxims of Epictetus and Pasteur echoed in my head:
“On the occasion of every accident that befalls you, remember to turn to yourself and inquire what power you have to turn it to use” and “Chance favors only the prepared mind.”
 
<center>[[File:Montante_plot2.png | 500px]]</center>
My “prepared” mind searched for answers, leading me down varied learning paths. Tapping the power of networks, I dropped a note to Chance News editor Bill Peterson. His quick web search surfaced a story from ''Nature News'' on research by Hans Herrmann, et. al. [http://www.nature.com/news/2004/040227/full/news040223-11.html Shattered eggs reveal secrets of explosions].  As described there, researchers have found power-law relationships for the fragments produced by shattering a pane of glass or breaking a solid object, such as a stone. Seems there is a science underpinning how things break and explode; potentially useful in Forensic reconstructions.
Bill also provided a link to [http://cran.r-project.org/web/packages/poweRlaw/vignettes/poweRlaw.pdf a vignette from CRAN] describing a maximum likelihood procedure for fitting a Power Law relationship. I am now learning my way through that.
 
Submitted by William Montante
 
----

Latest revision as of 20:58, 17 July 2019


Forsooth

Quotations

“We know that people tend to overestimate the frequency of well-publicized, spectacular events compared with more commonplace ones; this is a well-understood phenomenon in the literature of risk assessment and leads to the truism that when statistics plays folklore, folklore always wins in a rout.”

-- Donald Kennedy (former president of Stanford University), Academic Duty, Harvard University Press, 1997, p.17

"Using scientific language and measurement doesn’t prevent a researcher from conducting flawed experiments and drawing wrong conclusions — especially when they confirm preconceptions."

-- Blaise Agüera y Arcas, Margaret Mitchell and Alexander Todoorov, quoted in: The racist history behind facial recognition, New York Times, 10 July 2019

In progress

What if the Placebo Effect Isn’t a Trick?
by Gary Greenberg, New York Times Magazine, 7 November 2018

The Problems With Risk Assessment Tools
by Chelsea Barabas, Karthik Dinakar and Colin Doyle, New York Times, 17 July 2019

Hurricane Maria deaths

Laura Kapitula sent the following to the Isolated Statisticians e-mail list:

[Why counting casualties after a hurricane is so hard]
by Jo Craven McGinty, Wall Street Journal, 7 September 2018

The article is subtitled: Indirect deaths—such as those caused by gaps in medication—can occur months after a storm, complicating tallies

Laura noted that

Did 4,645 people die in Hurricane Maria? Nope.
by Glenn Kessler, Washington Post, 1 June 2018

The source of the 4645 figure is a NEJM article. Point estimate, the 95% confidence interval ran from 793 to 8498.

President Trump has asserted that the actual number is 6 to 18. The Post article notes that Puerto Rican official had asked researchers at George Washington University to do an estimate of the death toll. That work is not complete. George Washington University study

We sttill don’t know how many people died because of Katrina
by Carl Bialik, FiveThirtyEight, 26 August 2015

These 3 Hurricane Misconceptions Can Be Dangerous. Scientists Want to Clear Them Up.
Misinterpretations of the “Cone of Uncertainty” in Florida during the 2004 Hurricane Season
Definition of the NHC Track Forecast Cone

Remember when a glass of wine a day was good for you? Here's why that changed. Popular Science, 10 September 2018

Googling the news
Economist, 1 September 2018

We sat in on an internal Google meeting where they talked about changing the search algorithm — here's what we learned

Reading , Writing and Risk Literacy

[1]

Today is the deadliest day of the year for car wrecks in the U.S.

Some math doodles

<math>P \left({A_1 \cup A_2}\right) = P\left({A_1}\right) + P\left({A_2}\right) -P \left({A_1 \cap A_2}\right)</math>

<math>P(E) = {n \choose k} p^k (1-p)^{ n-k}</math>

<math>\hat{p}(H|H)</math>

<math>\hat{p}(H|HH)</math>

Accidental insights

My collective understanding of Power Laws would fit beneath the shallow end of the long tail. Curiosity, however, easily fills the fat end. I long have been intrigued by the concept and the surprisingly common appearance of power laws in varied natural, social and organizational dynamics. But, am I just seeing a statistical novelty or is there meaning and utility in Power Law relationships? Here’s a case in point.

While carrying a pair of 10 lb. hand weights one, by chance, slipped from my grasp and fell onto a piece of ceramic tile I had left on the carpeted floor. The fractured tile was inconsequential, meant for the trash.

BrokenTile.jpg

As I stared, slightly annoyed, at the mess, a favorite maxim of the Greek philosopher, Epictetus, came to mind: “On the occasion of every accident that befalls you, turn to yourself and ask what power you have to put it to use.” Could this array of large and small polygons form a Power Law? With curiosity piqued, I collected all the fragments and measured the area of each piece.

Piece Sq. Inches % of Total
1 43.25 31.9%
2 35.25 26.0%
3 23.25 17.2%
4 14.10 10.4%
5 7.10 5.2%
6 4.70 3.5%
7 3.60 2.7%
8 3.03 2.2%
9 0.66 0.5%
10 0.61 0.5%
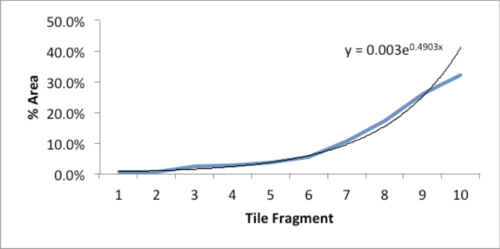
Montante plot1.png

The data and plot look like a Power Law distribution. The first plot is an exponential fit of percent total area. The second plot is same data on a log normal format. Clue: Ok, data fits a straight line. I found myself again in the shallow end of the knowledge curve. Does the data reflect a Power Law or something else, and if it does what does it reflect? What insights can I gain from this accident? Favorite maxims of Epictetus and Pasteur echoed in my head: “On the occasion of every accident that befalls you, remember to turn to yourself and inquire what power you have to turn it to use” and “Chance favors only the prepared mind.”

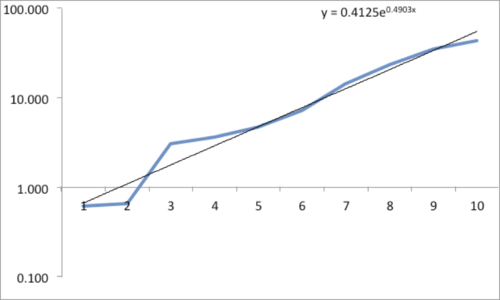
Montante plot2.png

My “prepared” mind searched for answers, leading me down varied learning paths. Tapping the power of networks, I dropped a note to Chance News editor Bill Peterson. His quick web search surfaced a story from Nature News on research by Hans Herrmann, et. al. Shattered eggs reveal secrets of explosions. As described there, researchers have found power-law relationships for the fragments produced by shattering a pane of glass or breaking a solid object, such as a stone. Seems there is a science underpinning how things break and explode; potentially useful in Forensic reconstructions. Bill also provided a link to a vignette from CRAN describing a maximum likelihood procedure for fitting a Power Law relationship. I am now learning my way through that.

Submitted by William Montante

Retrieved from "https://www.causeweb.org/wiki/chance/index.php?title=Sandbox&oldid=22455"