Chance News 95: Difference between revisions
| (6 intermediate revisions by one other user not shown) | |||
| Line 41: | Line 41: | ||
<div align=center>“Figure 2. Q-Q plots of Z scores for telomeric interval-length differences.”</div><br> | <div align=center>“Figure 2. Q-Q plots of Z scores for telomeric interval-length differences.”</div><br> | ||
<div align=right>Cited as #8 of [http://www.biostat.wisc.edu/~kbroman/topten_worstgraphs/ “The top ten worst graphs”]<br> | <div align=right>Cited as #8 of [http://www.biostat.wisc.edu/~kbroman/topten_worstgraphs/ “The top ten worst graphs”]<br> | ||
from [http://www.ncbi.nlm.nih.gov/pubmed/15627237?dopt=Abstract “Ethnicity and Human Genetic Linkage Maps”] | from [http://www.ncbi.nlm.nih.gov/pubmed/15627237?dopt=Abstract “Ethnicity and Human Genetic Linkage Maps”]<br> | ||
<i>American Journal of Human Genetics</i>, February 2005</div> | |||
| Line 161: | Line 162: | ||
''Revolutions'' blog (Revolution Analytics), 7 October 2013 | ''Revolutions'' blog (Revolution Analytics), 7 October 2013 | ||
This post presents another example of the paradox. Since 2000, median wages have | This post presents another example of the paradox. Since 2000, median wages in the US have increased by 1% overall, but have decreased for all educational subgroups. The explanation is the size of the subgroups: the population is becoming more educated, and wages tend to increase with education. (A related trend involving unemployment data from a 2009 ''Wall Street Journal'' article was discussed in Chance News [http://test.causeweb.org/wiki/chance/index.php/Chance_News_58#Simpson.E2.80.99s_Paradox_in_the_news here].) | ||
There is also an extended discussion of the famous 1973 UC Berkeley graduate school admissions data, and a link to [http://vudlab.com/simpsons/ an interactive graphic] that illustrates how the paradox arises in that example. | There is also an extended discussion of the famous 1973 UC Berkeley graduate school admissions data, and a link to [http://vudlab.com/simpsons/ an interactive graphic] that illustrates how the paradox arises in that example. | ||
| Line 257: | Line 258: | ||
Here is another video. Albert Kim sent this reference to the Isolated Statisticians list. The article describes the Central Limit Theorem and links to a nice 4-minute video that illustrates the distribution of the sample mean when sampling from normal (bunnies) and non-normal (dragons) populations. Students in introductory statistics often struggle with the idea of a sampling distribution. The animation here can help with the intuition. | Here is another video. Albert Kim sent this reference to the Isolated Statisticians list. The article describes the Central Limit Theorem and links to a nice 4-minute video that illustrates the distribution of the sample mean when sampling from normal (bunnies) and non-normal (dragons) populations. Students in introductory statistics often struggle with the idea of a sampling distribution. The animation here can help with the intuition. | ||
'''Note'''. A more | '''Note'''. A more elaborate visual simulation of sampling distributions is given in a classic applet on [http://onlinestatbook.com/stat_sim/sampling_dist/index.html sampling distributions] from the Rice University Virtual Lab in Statistics (RVLS). It animates of the sampling distribution of the mean and other statistics from built-in or user-defined distributions. [From the larger project Online Statistics Education: A Multimedia Course of Study ([http://onlinestatbook.com/ onlinestatbook.com]). Project Leader: David M. Lane, Rice University.] | ||
==Measuring teacher quality== | ==Measuring teacher quality== | ||
Latest revision as of 19:18, 16 November 2013
August 21, 2013 to October 15, 2013
Quotations
“It is worth dwelling for a moment on Egon [son of Karl] Pearson’s first-year lecture course …. [H]e was an inspirational teacher …. What was the reason for his success? [H]e was not a teacher who ladled out cookery-book recipes; rather he always seemed in his lectures to be working through and exploring problems with the class. He would wander down enticing dead-ends, but return to seek alternatives again and again until a satisfactory approach had been established. The result was that students acquired a questioning approach, not a compartmentalized approach whereby one problem was allocated to a 2 x 2 table, the next to multiple linear regression, etc.”
(1994 presidential address to the RSS)
Submitted by Margaret Cibes
“In my own field of flood risks, a talented statistician declared: ‘It is also true that for extremely rare events, correct uncertainty estimates may lead us to conclude that we know virtually nothing. This is not such a bad thing. If we really know nothing we should say so!’”
Submitted by Margaret Cibes
“For emotionally significant events, the size of the probability simply doesn’t matter. What matters is the possibility of winning. People are excited by the image in their mind. The excitement grows with the size of the prize, but it doesn’t diminish with the size of the probability.”
Submitted by Bill Peterson
"Often what is important about a statistical method is not what it does with the data, but rather what data it uses."
Submitted by Paul Alper
Another quote from Andrew Gelman, with potential relevance beyond social science research papers ....
".... High-profile social science research aims for proof, not for understanding - and that's a problem. .... But the incentives also favor silly causal claims. In many social sciences, it's not enough to notice an interesting pattern and explore it .... Instead, you are supposed to make a strong causal claim, even in a context where it makes little sense. In summary, I see the ethical problem in our publication system, in which the appearance of definitive argument is valued over open exploration. Authors are encouraged to see potential criticisms not as open questions to pursue, but as 'threats to validity' to be quashed. .... A research paper is more than a series of hypotheses and a data dump."
Chance, 2013 (#2)
Submitted by Margaret Cibes
Forsooth
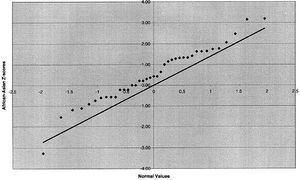
American Journal of Human Genetics, February 2005

The New York Times, August 24, 2013
Submitted by Margaret Cibes and James Greenwood
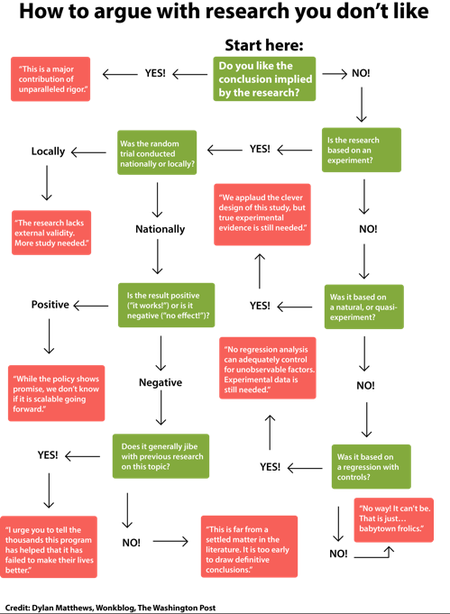
Washington Post Wonkblog, 12 September 2013
Submitted by Paul Alper
Weeding wedding invitation lists
“GUESTimation: Breaking the deadlock on wedding guest lists”
by Damjan Vukcevic, Significance, August 2013
Winner of the second annual Young Writers Competition, this article describes the process the author used to narrow his initial wedding guest list down to a number that his venue could accommodate. The process included grouping potential invitees (e.g., families), ranking them for their probabilities of attending if invited (to Australia), and using a probability distribution of the number of attendees to get a confidence interval of attendees. He also discusses his independence assumption and the consequence of using or not using it.
Submitted by Margaret Cibes
Civil rights and Simpson's paradox
Mary Parker sent this example of Simpson's Paradox to the Isolated Statisticians list:
Were Republicans really the party of civil rights in the 1960s?
by Harry J. Enten, Guardian, 28 August 2013
The 50th anniversary of the March on Washington and Martin Luther King's famous "I have a dream speech" have been commemorated in much recent news coverage. In light of some Republican claims that their record on civil rights compares favorably to Democrats, the Guardian takes a statistical look at the voting record on the landmark Civil RIghts Act of 1964.
The article presents 3 tables, which are reproduced below. The first breaks out the vote by party in the House of Representatives and the Senate, indicating that the bill had greater support among Republicans.
1964 Civil Rights Act Senate Version Ayes Democrats Republicans House 153 of 244 (63%) 136 of 171 (80%) Senate 46 of 67 (69%) 27 of 33 (82%)
The second table takes into account the history of the Civil War, separating out the 11 southern states that formed the Confederacy (note the remaining 39 states are classified as "Union", but of course not all of these current states existed in the 1860s).
1964 Civil Rights Act Senate Version Ayes Union Confederacy House 281 of 313 (90%) 8 of 102 (8%) Senate 72 of 78 (92%) 1 of 22 (5%)
Observing that political party and geography both matter, the Guardian's third table accounts for both:
1964 Civil Rights Act Senate Version Ayes Dem/Union Rep/Union Dem/Confed Rep/Confed House 145 of 152 (95%) 136 of 161 (85%) 8 of 91 (9%) 0 of 11 (0%) Senate 45 of 46 (98%) 27 of 32 (84%) 1 of 21 (5%) 0 of 1 (0%)
This gives an example of Simpson's Paradox. In both the north and the south, the bill had stronger support among Democrats than Republicans. However, aggregating over region leads to the first table, which reverses the direction of the association. The explanation is that a larger proportion of Democrats came from the south (in the House, 91 of the 244 Democrats came from the South, compared with only 11 of the 171 Republicans), where support for the Civil Rights Act was much weaker.
[Note. In the original Guardian article, the third table gives the Dem/Union count in the House as 144, which leaves the Aye total for Democrats one vote short of the first table. Nick Horton alertly noticed this and wrote to the author, who subsequently identified the missing vote as a Pennsylvania Democrat whose party affiliation was listed as "unknown" in one of the voting databases and erroneously wound up in Republican count. Thanks to Nick for communicating the correction to the Isolated Statisticians list.]
Simpson's and soccer
Jeff Witmer sent another example to the IsoStat list, this one involving accuracy of shots in soccer.
- By head or by foot, by Jamie Aspinall, Kickdex.com blog, 24 September 2013
Analysis of data from the 2012/13 English Premier League soccer season finds that, overall, headed shot were 4% more likely to be on goal than kicked shots, which sounds surprising. The lurking variable is the angle of view of the shooter to the goal. A larger proportion of headed-shots were taken straight towards the goal. Controlling for angle of the shot reveals that kicked shots are in fact more accurate at each shooting angle. This comparison was done by grouping the angles into 10-degree-wide bins.
The blog post linked above concludes with this comment:
The effect was even more pronounced when we applied the same approach to the fraction of attempts that actually resulted in a goal. The naive approach suggested that headers resulted in a goal 29% more often, however controlling for the angle of view revealed that they were actually 58% less likely to score.
In subsequent posts, we’ll seek to uncover the reasons for this difference. Is heading fundamentally a harder skill, or are there more variables lurking?
Discussion
What other possible lurking variables can you suggest?
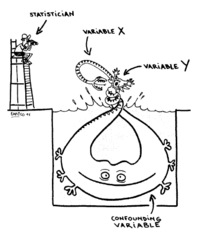
A visual exploration of Simpson's Paradox
An interactive tool to explain Simpson's Paradox
Revolutions blog (Revolution Analytics), 7 October 2013
This post presents another example of the paradox. Since 2000, median wages in the US have increased by 1% overall, but have decreased for all educational subgroups. The explanation is the size of the subgroups: the population is becoming more educated, and wages tend to increase with education. (A related trend involving unemployment data from a 2009 Wall Street Journal article was discussed in Chance News here.)
There is also an extended discussion of the famous 1973 UC Berkeley graduate school admissions data, and a link to an interactive graphic that illustrates how the paradox arises in that example.
Curious quotation on correlation
Margaret Cibes sent the following passage from The Big Short: Inside the Doomsday Machine, by Michael Lewis (Norton, 2011):
At issue was how highly correlated the prices of various subprime mortgage bonds inside a CDO might be. Possible answers ranged from zero percent (their prices had nothing to do with each other) to 100 percent (their prices moved in lockstep with each other). Moody’s and Standard Poor’s judged the pools of triple-B-rated bonds to have a correlation of around 30 percent, which did not mean anything like what it sounds. It does not mean, for example, that if one bond goes bad, there is a 30 percent chance that the others will go bad too. It means that if one bond goes bad, the others experience very little decline at all. [pp. 207-208, emphasis added]
Discussion
What do you make of the last sentence? Is this a Forsooth?
Cancer and height
Mike Olinick sent a link to the following, adding that it is instructive to look at the comments at the end of the article:
- Cancer risk increases with height
- by Tara Parker-Pope, New York Times Well blog, 25 July 2013.
A recent study (abstract here) of postmenopausal women has found a positive association between women's height and the risk for a number of cancers. A news release from the American Association for Cancer Research summarizes the study as follows
Height was linked to cancers of the breast, colon, endometrium, kidney, ovary, rectum, and thyroid, as well as to multiple myeloma and melanoma, and these associations did not change even after adjusting for factors known to influence these cancers, in this study of 20,928 postmenopausal women, identified from a large cohort of 144,701 women recruited to the Women’s Health Initiative (WHI).
Geoffrey Kabat, the lead author on the study, is quoted as saying, "We were surprised at the number of cancer sites that were positively associated with height. In this data set, more cancers are associated with height than were associated with body mass index [BMI].”
Noting that the reason for the association is not clear, the NYT post presents several speculative ideas. A larger body has a larger number of cells, which may represent more opportunities for cancerous cells to develop. Or perhaps the hormonal factors involved in normal growth can also stimulate malignancies. On the other hand, there are many potential confounding variables, such as diet. Quoting Dr Kabat, "Height itself is not a risk factor, but it really appears to be a marker for one or more exposures that influence cancer risk.”
In the comments section, one alert reader pointed out that similar results had been announced in 2011 in a study from the UK:
- Taller women more likely to develop cancer
- by Denis Campbell, The Guardian, 20 July 2011
This article proposes the same two possible explanations for the effect described above. It also answers a question that some of the NYT readers raised, namely how big is the effect? We read, "A woman's chances of developing cancer rose by 16% for every extra 10cm (4in) in height, found the study, which looked at 97,000 women with the disease between 5ft and 5ft 9in tall."
Discussion
A number of the comments at the NYT site are quite dismissive: "spurious correlation." On the other hand, we find two serious studies on the association. What do you make of this?
Talk and interview by Proofiness author
Charles Seife is the acclaimed author of Proofiness: The Dark Arts of Mathematical Deception. A Chance News review may be found here.
Here is a link to a video of his hour-long lecture given at Google’s New York office. The title of his presentation is “Context is Everything-More About the Dark Arts of Mathematical Deception.”
This web site also refers one to a 26 minute New Zealand radio interview which is entitled, “Numbers Don’t Lie, But People Do.”
Submitted by Paul Alper
US population pyramid - interactive over time
Margaret Cibes sent the following from the Daily Kos:
Demographics: Today's cool bit of data visualization comes from the Census Bureau, which has turned the nation's age and gender composition over the last century into an animation. The best part is watching the bulge from the Baby Boom generation pass through the century's midsection, much like watching a snake digest a rat.
Here is a static screen grab from 1999, but you should view the whole animation at the link above. See also the bottom of that page for links to other Census data visualizations.
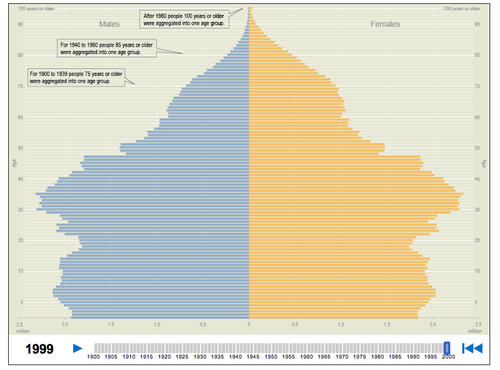
An earlier Chance News discussion of population pyramids can be found here. Included there is a link instructions for creating your own pyramid plots in R or SAS.
Radical cartography
On a related theme, Margaret sent the following examples from Bill Rankin's intriguing Radical Cartography website:
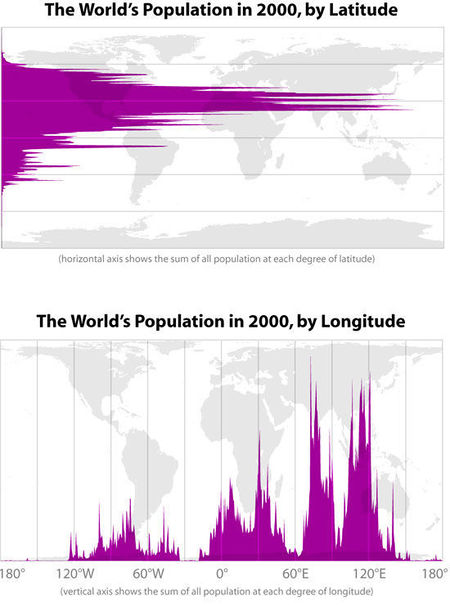
There are many great plots to explore here.
Coffee and a Forsooth!
Paul Alper sent the following Forsooth about coffee drinkers:
- "Men who drink more than four cups a day are 56 per cent more likely to die."
The quotation is from Coffee quaffers face increased death risk: study (New Zealand Herald, 18 September 2013). The study in question is Association of coffee consumption with all-cause and cardiovascular disease mortality (Mayo Clin Proc. 15 Aug 2013).
The whole discussion drew commentary on Andrew Gelman's blog Is coffee a killer? I don’t think the effect is as high as was estimated from the highest number that came out of a noisy study. Andrew observes that the Herald's claim of increased mortality risk, as quoted above, "is obviously not true: deaths, as we’ve observed before, are fixed at one per customer." He also writes:
On the plus side, it [the study] says “the statistics have been adjusted to remove the impact of smoking.” I hope they did a good job with that adjustment. Smoking is the elephant in the room. If you don’t adjust carefully for smoking and its interactions, you can pollute all the other estimates in your study.
Paul comments that "coffee drinking must be the most studied habit in the statistical world." He sent a link to a TED talk by Ben Goldacre contrasting various health conclusions. In the first minute Goldacre presents a slide where coffee is listed as both causing and curing cancer!
Goldacre is the author of the "Bad Science" column in The Guardian; some of these pieces have been mentioned in earlier Chance News. His web site includes archives of these articles and much more.
Statistics in dance?
“Statistics Explained Through Modern Dance”
Open Culture, October 1, 2013
Two British folks have produced four short films (3-5 minutes each) purporting to demonstrate the statistical concepts of (1) correlation, (2) frequency distributions, (3) sampling and standard error, and (4) variance. I’m not sure that they have discovered, as the subtitle indicates, “A New Way of Teaching a Tough Subject”; however, the correlation video was the most clearly illustrative of its topic, in my opinion.
Submitted by Margaret Cibes at the suggestion of Bilal Sekou
Rabbits, dragons and the Central Limit Theorem
As ‘normal’ as rabbits’ weights and dragons’ wings
By Casey Dunn, New York Times, 23 September 2013
Here is another video. Albert Kim sent this reference to the Isolated Statisticians list. The article describes the Central Limit Theorem and links to a nice 4-minute video that illustrates the distribution of the sample mean when sampling from normal (bunnies) and non-normal (dragons) populations. Students in introductory statistics often struggle with the idea of a sampling distribution. The animation here can help with the intuition.
Note. A more elaborate visual simulation of sampling distributions is given in a classic applet on sampling distributions from the Rice University Virtual Lab in Statistics (RVLS). It animates of the sampling distribution of the mean and other statistics from built-in or user-defined distributions. [From the larger project Online Statistics Education: A Multimedia Course of Study (onlinestatbook.com). Project Leader: David M. Lane, Rice University.]
Measuring teacher quality
Priscilla Bremser sent a link to the following:
- Measuring teacher quality, by David Bressoud, MAA Launchings column, July 2013.
In this column, Bressoud describes a 2010 study by Scott E. Carrell and James E. West Does professor quality matter? Evidence from random assignment of students to professors (Journal of Political Economy, University of Chicago Press, vol. 118(3), pages 409-432, 06).
There are several interesting design elements. The study looked at Calculus I classes at the US AIr Force Academy, where all students are required to take Calculus I, and can be randomly assigned to instructors. Bressoud explains that this mitigates the problem of selection bias, whereby the top students might seek out the best teachers. Also, the study considered student performance in the Calculus II sequel and found no evidence of "backward correlation," meaning that the ratings for those instructors were not associated with better performance in Calculus I.
Summarizing the results, Bressoud notes that the following attributes of Calculus I classes all had significant positive correlations with student performance:
- Instructor’s ability to provide clear, well-organized instruction.
- Value of questions and problems raised by instructor.
- Instructor’s knowledge of course material.
- The course as a whole.
- Amount you learned in the course.
- The instructor’s effectiveness in facilitating my learning in the course.
Interestingly, these same attributes for Calculus I were negatively associated with performance in Calculus II; for the first two attributes and the last, the correlations were significant. By contrast, faculty rank, highest degree attained, and years of experience of the Calculus I instructors had negative associations with performance in Calculus I, but positive associations with later performance in Calculus II.
Bressoud outlines one possible explanation for these trends: younger instructors may focus on immediate preparation for the next assignment or exam, whereas more experienced instructors may have better perspective and strive to prepare students for the longer haul. Naturally, the former approach might be more popular with students in the short term, leading to better end-of-course evaluations.