Chance News 63: Difference between revisions
| (11 intermediate revisions by 2 users not shown) | |||
| Line 90: | Line 90: | ||
===Discussion=== | ===Discussion=== | ||
1. Buried in the article: The total sample size of free throws attempted was 425, with 60, 121, 191, 22 and 9 representing 1, 2, 3, 4 and 7 dribbles for a total of 403. No information is given for 5 and 6 dribbles but from the data, the inference is that | 1. Buried in the article: The total sample size of free throws attempted was 425, with 60, 121, 191, 22 and 9 representing 1, 2, 3, 4 and 7 dribbles for a total of 403. No information is given for 5 and 6 dribbles but from the data, the inference is that they represent 22 (425-403) attempts. Given this data, how impressive does the 77% success rate for four dribbles appear? | ||
2. Why didn’t the author choose to present a simple table of number of dribbles, free-throw attempts, free-throws made instead of dribbling the information all over the article? Is any insight provided by the following graphic from the article? | 2. Why didn’t the author choose to present a simple table of number of dribbles, free-throw attempts, free-throws made instead of dribbling the information all over the article? Is any insight provided by the following graphic from the article? | ||
| Line 124: | Line 124: | ||
For example, the article cites the following misinterpretation of significance at the 5% level: “This means that it is 95 percent certain that the observed difference between groups, or sets of samples, is real and could not have arisen by chance.” Indeed, versions of this are all too often seen in print! | For example, the article cites the following misinterpretation of significance at the 5% level: “This means that it is 95 percent certain that the observed difference between groups, or sets of samples, is real and could not have arisen by chance.” Indeed, versions of this are all too often seen in print! | ||
Also discussed are the multiple comparisons problem, the challenges of interpreting meta-analyses | Also discussed are the multiple comparisons problem and the "false discovery rate", the challenges of interpreting meta-analyses; and the disagreements between frequentists and Bayesians. | ||
Submitted by Bill Peterson, based on a suggestion from Scott Pardee | Submitted by Bill Peterson, based on a suggestion from Scott Pardee | ||
'''Discussion | '''Discussion Question''' | ||
Box 2, paragraph 1 of the article states "Actually, the P value gives the probability of observing a result if the null hypothesis is true, and there is no real effect of a treatment or difference between groups being tested. A P value of .05, for instance, means that there is only a 5 percent chance of getting the observed results if the null hypothesis is correct." Why is this statement wrong? | |||
Submitted by Bill Jefferys | |||
==Global data graphics== | ==Global data graphics== | ||
| Line 209: | Line 211: | ||
by Steven Strogatz, ''New York Times'', Opinionator blog, 25 April 2010 | by Steven Strogatz, ''New York Times'', Opinionator blog, 25 April 2010 | ||
Steven Strogatz, an applied mathematics professor at Cornell University, has been writing engaging weekly installments about mathematics for the Opinionator. His post this week is about probability; more specifically, it focuses on conditional probability. Of course, this topic is a notorious source of confusion. | Steven Strogatz, an applied mathematics professor at Cornell University, has been writing engaging weekly installments about mathematics for the Opinionator. His post this week is about probability; more specifically, it focuses on conditional probability. Of course, this topic is a notorious source of confusion. Indeed, this edition of Chance News includes [http://www.causeweb.org/wiki/chance/index.php/Chance_News_63#Bird_brains_vs._birdbrains another appearance of the Monty Hall problem], which stubbornly refuses to stay solved. | ||
The article presents several famous examples, including the false positive problem in diagnostic medical screening, and the conflicting arguments over spousal abuse and murder at the the O.J. Simpson trial. Strogatz expresses enthusiasm for the approach of Gerd Gigerenzer, a psychologist who has argued that describing such problems in terms of "natural frequencies" rather than conditional probabilities helps people reason more clearly (Gigerenzer's book ''Calculated Risks: How to Know When Numbers are Deceiving You'' was discussed in [http://www.causeweb.org/wiki/chance/index.php/Chance_News_14#Gerd_Gigerenzer.27s_Calculated_Risks_Revisited Chance News 14]). Essentially, this approach involves thinking about the problem in terms of a hypothetical cohort large enough to clear the denominators from the fractions, so one is talking about whole numbers of cases and the relevant ratios become easier to visualize. | The article presents several famous examples, including the false positive problem in diagnostic medical screening, and the conflicting arguments over spousal abuse and murder at the the O.J. Simpson trial. Strogatz expresses enthusiasm for the approach of Gerd Gigerenzer, a psychologist who has argued that describing such problems in terms of "natural frequencies" rather than conditional probabilities helps people reason more clearly (Gigerenzer's book ''Calculated Risks: How to Know When Numbers are Deceiving You'' was discussed in [http://www.causeweb.org/wiki/chance/index.php/Chance_News_14#Gerd_Gigerenzer.27s_Calculated_Risks_Revisited Chance News 14]). Essentially, this approach involves thinking about the problem in terms of a hypothetical cohort large enough to clear the denominators from the fractions, so one is talking about whole numbers of cases and the relevant ratios become easier to visualize. | ||
| Line 218: | Line 220: | ||
==Media Highlights from College Mathematics Journal== | ==Media Highlights from College Mathematics Journal== | ||
We have often mentioned in Chance News, articles from the Media Highlights section of the College Mathematics Journal that we thought our readers would enjoy reading. We were pleased to see that the May 2010 issue of this Journal included in their Media Highlights an expanded version of a Chance News article "Simpson's Paradox" contributed by Margaret Cibes in Chance News | We have often mentioned in Chance News, articles from the Media Highlights section of the College Mathematics Journal that we thought our readers would enjoy reading. We were pleased to see that the May 2010 issue of this Journal included in their Media Highlights an expanded version of a Chance News article "Simpson's Paradox" contributed by Margaret Cibes in Chance News 58. In this Media Highlights they also discussed the following article from Nature Magazine<br> | ||
[http://www.nature.com/nature/journal/v461/n7266/full/461879a.html Massively collaborative mathematics ]<br> | [http://www.nature.com/nature/journal/v461/n7266/full/461879a.html Massively collaborative mathematics ]<br> | ||
| Line 249: | Line 251: | ||
Submitted by Paul Alper | Submitted by Paul Alper | ||
==Higher grades at private schools== | |||
[http://economix.blogs.nytimes.com/2010/04/19/want-a-higher-g-p-a-go-to-a-private-college/?scp=1&sq=gpa&st=cse “Want a Higher G.P.A.? Go to a Private College”]<br> | |||
by Catherine Rampell, <i>The New York Times</i>, April 19, 2010<br> | |||
Motivated by their concern about the disproprotionate representation of private-school students in science/engineering doctoral programs, two researchers studied average undergrad GPAs at private and public colleges/universities.<br> | |||
See a report of their study, [http://www.gradeinflation.com/tcr2010grading.pdf “Grading in American Colleges and Universities”]. The report indicates that the researchers looked at “contemporary” grades from over 160 colleges/universities, as well as the “historical” grades from over 80 schools. | |||
<center> | |||
http://graphics8.nytimes.com/images/2010/03/08/business/economy/gradeinflation.jpg | |||
</center> | |||
Unsurprisingly, they also found that science departments grade lower, on average, than humanities and social science departments (by 0.4 and 0.2 points, respectively).<br> | |||
See a website[http://www.gradeinflation.com] with detailed discussion, graphs and raw data, especially about individual schools. The website provides the following statement: | |||
<blockquote>As a rough rule of thumb, the average GPA of a school today can be estimated by the rejection percentage of its applicant pool:<br> | |||
GPA = 2.8 + Rejection Percentage /200 + (if the school is private add 0.2)</blockquote> | |||
Submitted by Margaret Cibes, based on an ISOSTAT posting | |||
Latest revision as of 16:06, 6 May 2010
Quotations
Everyone is entitled to his own opinions, but not his own facts.
Daniel Patrick Moynihan
As quoted in Believing Weird Things is Dangerous, Rob Breakenridge, The Calgary Herald, April 13, 2010.
Submitted by Steve Simon
It’s like buying fire insurance on your neighbor’s house — you create an incentive to burn down the house.
Philip Gisdakis, head of credit strategy at UniCredit in Munich
Quoted in the context of the Greek credit crisis (Banks bet Greece defaults on debt they helped hide, New York Times, 24 February 2010). But suddenly relevant again in light of recent SEC allegations against Goldman Sachs.
Submitted by Bill Peterson
Forsooth
A survey released by researchers at George Mason University found that more than a quarter of television weathercasters agree with the statement “Global warming is a scam,” and nearly two-thirds believe that, if warming is occurring, it is caused “mostly by natural changes.” (The survey also found that more than eighty per cent of weathercasters don’t trust “mainstream news media sources,” though they are presumably included in this category.)
Elizabeth Kolbert, The New Yorker
April 12, 2010
Submitted by Margaret Cibes
HIV patients in low socio-eonomic classes are 89 per cent more likely to die than better-off people with the infection, claims a study of 2684 adults in the Journal of Health Care for the Poor and Underserved (Nov).
The Times
8 November 2005
There are now more overweight people in America than average-weight people. So overweight people are now average. Which means you've met your New Year's resolution.
Jay Leno reported in the Cork Evening Echo
8 September 2007
The following 2 forsooths are from the April 2010 RRS News
British experts studied more than 17,000 children born in 1970
for about four decades. Of the children who ate candies or chocolates
daily at age 10, 69 percent were later arrested for a violent offence by the age of 34.
Of those who didn't have any violent clashes, 42 per cent ate sweets daily.
Northern Territory News
2 October 2009
A separate opinion poll yesterday suggested that 50% of
obese people earn less than the national average income..
The Guardian
3 November 2009
Submitted by Laurie Snell
From an interview with a con man who claims he can provide a stem-cell cure for diseases such as ALS and Alzeimer's:
Interviewer: “You told these men in Houston that a cure was, in a memorable phrase, 100% possible.”
Con man: “Possible. Is that a guarantee?”
60 Minutes, CBS
April 18, 2010
Submitted by Margaret Cibes
Of the 29,000 people who may get cancer from CT scans done in 2007, about 50 percent will die, the researchers estimated.
Nicole Ostrow, Bloomberg.com
December 14, 2009
Submitted by Margaret Cibes
Tiger’s effect on opponents
“Superstar Effect”
by Jonah Lehrer, The Wall Street Journal, April 3, 2010
Lehrer, author of How We Decide[1], states:
While challenging competitions are supposed to bring out our best, … studies demonstrate that when people are forced to compete against a peer who seems far superior, they often don't rise to the challenge. Instead, they give up.
The article is based, for the most part, on the paper “Quitters Never Win: The (Adverse) Incentive Effects of Competing with Superstars”, by Jennifer Brown, Northwestern University, September 2008. The paper includes detailed descriptive and inferential statistics.
Brown chose to study golf mainly because of the presence of Tiger Woods, whose playing dominates the game. She looked at data from professional golfers and found that the presence of Tiger Woods in a tournament resulted in the other golfers, taking, on average, 0.2 more strokes in the initial 18 holes and 0.8 more strokes in the whole tournament. (Note that Lehrer cites the figure 0.3 instead of Brown’s figure, 0.2.)[2]
Brown’s results apply to a field called economic tournament theory that investigates competitions in which relative, instead of absolute, performance is rewarded. She feels that the superstar effect is strongest when “there is a nonlinear incentive structure,” that is, when there is an extra incentive to finish first.
Lehrer also refers to a 2009 study[3] by University of Chicago psychologist Sian Beilock, who examined “choking” during golf competitions, possibly due to golfers over-thinking their actions.
We bring expert golfers into our lab, we tell them to pay attention to a particular part of their swing, and they just screw up. …When you are at a high level, your skills become somewhat automated. You don't need to pay attention to every step in what you're doing. ….
Lehrer concludes:
Regardless of the precise explanation for the superstar effect—are golfers quitting on themselves or thinking too much?
A blogger commented[4]:
But even the best do not intimidate every opponent. Ali did not intimidate Frazier, Federer did not intimidate Nadal (in fact it was the other way around until Nadal was weakened by injuries). Even Michael Jordan wasn't intimidating when he played without Scottie Pippen.
Submitted by Margaret Cibes
Dribbling data
"At the Free-Throw Line, 1...2...3...4 Whoosh"
by David Biderman, The Wall Street Journal, April 3, 2010
The author reports that, of the 425 free-throw attempts in the past 10 NCAA title games, players who dribbled 1, 2, 3, or 5 or more times before shooting were successful 60%, 66%, 68%, and 68% of the time, respectively, while those who dribbled 4 times were successful 77% of the time. Also, there were more NBA all-stars in the 4-dribble group than in any other group.
Submitted by Margaret Cibes
Discussion
1. Buried in the article: The total sample size of free throws attempted was 425, with 60, 121, 191, 22 and 9 representing 1, 2, 3, 4 and 7 dribbles for a total of 403. No information is given for 5 and 6 dribbles but from the data, the inference is that they represent 22 (425-403) attempts. Given this data, how impressive does the 77% success rate for four dribbles appear?
2. Why didn’t the author choose to present a simple table of number of dribbles, free-throw attempts, free-throws made instead of dribbling the information all over the article? Is any insight provided by the following graphic from the article?
http://sg.wsj.net/public/resources/images/PT-AO308_COUNT_NS_20100402163830.gif
3. The headline in the print edition, but not in the online edition is, "At the Foul Line, Four is the Magic Number." Comment on the "magicness" of four given the actual data.
Submitted by Paul Alper
Bird brains vs. birdbrains
“Mathematicians vs. Birds vs. Monty Hall”
by Tom Bartlett, The Chronicle of Higher Education, March 17, 2010
“Pigeons Beat Humans at Solving ‘Monty Hall’ Problem”
by Charles Q. Choi, Live Science, March 3, 2010
In the February 2010 issue of the Journal of Comparative Psychology, two Whitman College researchers reported about their work comparing the success rates of 6 pigeons and 12 undergraduate student volunteers in solving the Monty Hall problem[5] by trial and error:
By day 30 of the experiment, the pigeons had “learned” to adopt the best, “switch,” strategy “96 percent of the time.” However, the students had not found the best strategy “even after 200 trials of practice each.”
See an abstract[6] of the paper “Are birds smarter than mathematicians?”
Submitted by Margaret Cibes, based on an ISOSTAT posting
Odds are, it's wrong
Odds are, it's wrong
by Tom Siegfried, Science News, 27 March 2010
This is a long and provocative essay on the limitations of significance testing in scientific research. The main themes are that it is easy to do the such tests incorrectly, and, even when they are done correctly, they are subject to widespread misinterpretation.
For example, the article cites the following misinterpretation of significance at the 5% level: “This means that it is 95 percent certain that the observed difference between groups, or sets of samples, is real and could not have arisen by chance.” Indeed, versions of this are all too often seen in print!
Also discussed are the multiple comparisons problem and the "false discovery rate", the challenges of interpreting meta-analyses; and the disagreements between frequentists and Bayesians.
Submitted by Bill Peterson, based on a suggestion from Scott Pardee
Discussion Question
Box 2, paragraph 1 of the article states "Actually, the P value gives the probability of observing a result if the null hypothesis is true, and there is no real effect of a treatment or difference between groups being tested. A P value of .05, for instance, means that there is only a 5 percent chance of getting the observed results if the null hypothesis is correct." Why is this statement wrong?
Submitted by Bill Jefferys
Global data graphics
“Hans Rosling shows the best stats you’ve ever seen”
TEDTalk, February 2006
Hans Rosling[7] is global health professor and co-founder of Doctors without Borders Sweden, as well as a very entertaining speaker.
In this 20-minute YouTube video, he addresses “common myths about the so-called developing world,” based on animated graphs of UN data over time. Viewers will see “moving bubbles and flowing curves that make global trends clear, intuitive and even playful,” thanks to the free visualization software he has developed. (Full screen view is recommended.)
See also Rosling’s website, Gapminder[8], for lots more information and data.
Submitted by Margaret Cibes, based on an ISOSTAT posting
See also here [9] . Laurie Snell
Optimism of financial analysts
“Dow Loses Points, but Reader Wins 10-Year-Old Bet”
The Atlantic, May 2010
More than 10 years ago The Atlantic printed an article by the co-authors of a “new” theory of stock valuation, which included a prediction that the DJIA would rise from 11,453 at the end of 1999 to about 36,000 by the end of 2009. A reader wrote the magazine, calling the theory “a giant fallacy” and betting the authors that the Dow would be closer to 11,000 in 10 years.
The two authors agreed to the following bet:
If the Dow is closer to 10,000 than to 36,000 ten years from now, we will each give $1,000 to the charity of your choice.
After the Dow closed at 10,428 on December 31, 2009, the co-authors each donated $1,000 to the Salvation Army, the letter writer’s charity of choice.
It’s been a bad run for optimists,” [a co-author] noted.
The letter writer stated:
I’m surprised at the way it turned out. I thought their theory was pretty extreme, and that was the point of my letter …. I never imagined the Dow would have been less than in 1999. In a way, I was probably just as wrong as [the co-authors] were. If someone had bet me it would be lower, I would have taken the bet and lost it. Everybody lost on that one.
Submitted by Margaret Cibes
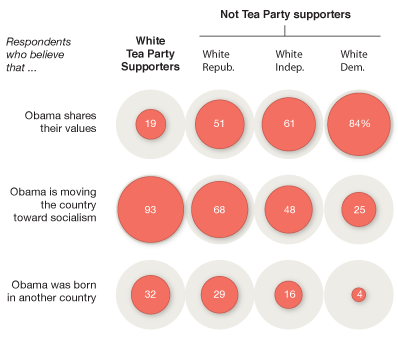
Tea party graphics
A mighty pale tea
by Charles M. Blow, New York Times, 16 April 2010
This article recounts Blow's experience visiting a Tea Party rally as a self-identified "infiltrator." He was interested in assessing the group's diversity. Reproduced below is a portion of a graphic, entitled The many shades of whites, that accompanied the article.
The data are from a recent NYT/CBS Poll.
Submitted by Paul Alper
Puzzles
Jessica Pittman is an education major doing an assistantship under a math teacher. She found Chance News very helpful but also noted that the link to a puzzle website referred to in Chance News 10.02 no longer exists. She suggests a similar website here as a replacement.
Submitted by Laurie Snell
NFL draft akin to coin toss
“A 50% Chance You’ll Squander Millions”
by Michael Salfino, The Wall Street Journal, April 21, 2010
According to an April 2010 Yale School of Management study, “The Loser’s Curse: Overconfidence vs. Market Efficiency in the National Football League Draft”,
[A]ny player called to the podium in the first five picks of the draft has about a 50% chance of being a flop.
Of the top five picks from 1991 through 2004, 10 (14%) did not play at least five years, 26 (37%) were/are still in the league after five years but never made a Pro Bowl, and 34 (49%) made at least one Pro Bowl.
The article contains an interactive graphic, “The Best NFL Prospects Pound-for-Pound”, in which the reader can choose one of five physical tests (40-year dash, bench press, broad jump, vertical jump, three-cone), and see the each draft pick’s performance on that test (as z-scores based on all 70 picks). Players are categorized by team position (5 defensive and 4 offensive positions).
Submitted by Margaret Cibes
NFL draft as simultaneous auction
“Why the NFL Draft Drives Economists Crazy”
by Reed Albergotti, The Wall Street Journal, April 22, 2010
Because the worst league teams get the first picks, it often “forces them to draft players they don't really need at prices they can't afford … [and m]any top picks hold out of training camp before they sign, only to end up with enormous contracts that have little to do with their true value to a football team.” One NFL executive is quoted:
"There's a huge trail littered with guys who got the big dollars but were a bust.
One problem with the current 75-year-old system is that the college game has changed significantly from a professional game. Another is that it is difficult to evaluate a player’s worth on the open market.
A team of WSJ and Harvard researchers have proposed using a “simultaneous ascending auction[, which] involves every NFL team bidding on all college players at the same time.” See
“Redrafting the Draft”, an interactive graphic that shows a mock auction detailing how the bottom-ranked St. Louis Rams might fare in this system.
Three Harvard Business School researchers have proposed giving each of the 32 teams seven picks, with spending caps on a sliding scale, in which the worst team would have the highest spending cap. Teams could raise their bids in competition for the most desirable picks, but that would have to be done within their spending caps.
Submitted by Margaret Cibes
Demystifying conditional probability?
Chances are
by Steven Strogatz, New York Times, Opinionator blog, 25 April 2010
Steven Strogatz, an applied mathematics professor at Cornell University, has been writing engaging weekly installments about mathematics for the Opinionator. His post this week is about probability; more specifically, it focuses on conditional probability. Of course, this topic is a notorious source of confusion. Indeed, this edition of Chance News includes another appearance of the Monty Hall problem, which stubbornly refuses to stay solved.
The article presents several famous examples, including the false positive problem in diagnostic medical screening, and the conflicting arguments over spousal abuse and murder at the the O.J. Simpson trial. Strogatz expresses enthusiasm for the approach of Gerd Gigerenzer, a psychologist who has argued that describing such problems in terms of "natural frequencies" rather than conditional probabilities helps people reason more clearly (Gigerenzer's book Calculated Risks: How to Know When Numbers are Deceiving You was discussed in Chance News 14). Essentially, this approach involves thinking about the problem in terms of a hypothetical cohort large enough to clear the denominators from the fractions, so one is talking about whole numbers of cases and the relevant ratios become easier to visualize.
For another recent discussion, see the section on Probabilities vs. Frequencies in John Allen Paulos's Who's Counting column from January, Medical statistics don't always mean what they seem to mean.
Submitted by Bill Peterson, based on a suggestion from Dan Bent (an intro statistics student)
Media Highlights from College Mathematics Journal
We have often mentioned in Chance News, articles from the Media Highlights section of the College Mathematics Journal that we thought our readers would enjoy reading. We were pleased to see that the May 2010 issue of this Journal included in their Media Highlights an expanded version of a Chance News article "Simpson's Paradox" contributed by Margaret Cibes in Chance News 58. In this Media Highlights they also discussed the following article from Nature Magazine
Massively collaborative mathematics
Timothy Glowers and Michael Nielson
Nature 461 (October 15, 2009.
This is about the Polymath Project described by Timothy Glowers as follows:
On 27 January 2009, one of us — Gowers — used his blog to announce an unusual experiment. The Polymath Project had a conventional scientific goal: to attack an unsolved problem in mathematics. But it also had the more ambitious goal of doing mathematical research in a new way. Inspired by open-source enterprises such as Linux and Wikipedia, it used blogs and a wiki to mediate a fully open collaboration. Anyone in the world could follow along and, if they wished, make a contribution. The blogs and wiki functioned as a collective short-term working memory, a conversational commons for the rapid-fire exchange and improvement of ideas.
The article goes on to describe the success that the Polymath Project made when they first started and what their hopes for the future are. If a success, this method could be applied to other forms of science. Of course the isolated statisticians group has some similarly here but it is not open to all.
Submitted by Laurie Snell
Lucky charms and disappointing journalism
The power of lucky charms: New research suggests how they really make us perform better
by Carl Bialik, Wall Street Journal, 28 April 2010
The headline of the article is eye-catching. The descriptions of the success or failure of the lucky charms is, however, an indictment of the way the journalism profession discusses statistics. Especially because the author, Carl Bialik, unlike most journalists, knows better. In fact, while his first paragraph tries to draw the reader in with “Can luck really influence the outcome of events,” his second paragraph begins with “They [lucky charms] do (sometimes)” as a means of absolving himself from taking the material seriously.
In silly instance after silly unreplicated instance, the article tells us that averages improve or don’t improve with lucky charms present, but never once do we know anything about the variability between the charm holders and those deprived of the lucky charms.
Discussion Questions
1. The first example referred to will be published in the June issue of Psychological Science; the study involves 28 German college students whose putting with a “lucky ball” sank “6.4 putts out of 10, nearly two more putts, on average, than those who weren’t told the ball was lucky.” Evaluate the comment, “but the effect was big enough to be statistically significant.” What additional statistical information would be necessary to view this study as worthwhile?
2. A well known quotation in the field of statistics is “The plural of anecdote is not evidence.” Read the article and evaluate the anecdotes.
3. Superstition plays a vital part of this article: a motorcyclist who wears “gremlin balls” to “help ward off accidents”; a lucky brown suit “to help the horse he co-owns, Always a Party, win the second race”; after an eclipse, “major U.S. stock-market indexes typically fall.” Compare those superstitions with the reading of tea leaves and goat entrails of the middle ages.
Submitted by Paul Alper
Higher grades at private schools
“Want a Higher G.P.A.? Go to a Private College”
by Catherine Rampell, The New York Times, April 19, 2010
Motivated by their concern about the disproprotionate representation of private-school students in science/engineering doctoral programs, two researchers studied average undergrad GPAs at private and public colleges/universities.
See a report of their study, “Grading in American Colleges and Universities”. The report indicates that the researchers looked at “contemporary” grades from over 160 colleges/universities, as well as the “historical” grades from over 80 schools.
http://graphics8.nytimes.com/images/2010/03/08/business/economy/gradeinflation.jpg
Unsurprisingly, they also found that science departments grade lower, on average, than humanities and social science departments (by 0.4 and 0.2 points, respectively).
See a website[10] with detailed discussion, graphs and raw data, especially about individual schools. The website provides the following statement:
As a rough rule of thumb, the average GPA of a school today can be estimated by the rejection percentage of its applicant pool:
GPA = 2.8 + Rejection Percentage /200 + (if the school is private add 0.2)
Submitted by Margaret Cibes, based on an ISOSTAT posting