Chance News 22: Difference between revisions
No edit summary |
|||
| Line 147: | Line 147: | ||
One of the first studies of this kind was suggested by asking similar questions about the number of different species of butterflies in Malaya and was reported in the paper | One of the first studies of this kind was suggested by asking similar questions about the number of different species of butterflies in Malaya and was reported in the paper | ||
"The Relation Between the Number of Species and the Number of Individuals in a | "The Relation Between the Number of Species and the Number of Individuals in 1943 in a paper by R.A. Fisher, A.A. Corbet and C. B. Williams.(1) | ||
The authors write: | The authors write: | ||
| Line 309: | Line 309: | ||
</center> | </center> | ||
Wang and Dodson were interested in finding the number of species (in their case genera) that have not been observed in previous samples. This problem was first studied by I. J. Good and G. H. Tollmin | Wang and Dodson were interested in finding the number of species (in their case genera) that have not been observed in previous samples. This problem was first studied in 1953 by I. J. Good (2) and in 1956 by I.J. Goode and G. H. Tollmin (3) Bradley Efron and Ronals Thisted used the methods developed by Good and Tollmin to answer two questions provided in the titles of the two papers they wrote; | ||
Efron and Thisted considered the words in Shakespeare's as species and took as the first sample Shakespear's know works which comprised of 884,647 using their convention when two words are different they found 31,534 different words. The provided a table showing the number of words that accored once, twice, three times ect. up to 100. Following Fisher they assumed that for the first sample the number of times that a word occurs s has a Poisson distribution with mean <math>\lambda_s</math> which is proportional to the size of the sample. Like Fisher they assumed that <math>\lambda_s</math> is a random variable but unlike Fisher they did not assume that they knew its distribution but rather used an imperical distribution obtained from the data. They then consider a second sample with sample size a multiple t of the first sample and calcultate the expected number of words that will occur in this sample that did not occur in the first sample. They find that if they take a sample the size of his known works the expected number of new words would be 11,430 which can be considered to be a lower bound on the number of additional words that Shakespeare knew. | Efron and Thisted considered the words in Shakespeare's as species and took as the first sample Shakespear's know works which comprised of 884,647 using their convention when two words are different they found 31,534 different words. The provided a table showing the number of words that accored once, twice, three times ect. up to 100. Following Fisher they assumed that for the first sample the number of times that a word occurs s has a Poisson distribution with mean <math>\lambda_s</math> which is proportional to the size of the sample. Like Fisher they assumed that <math>\lambda_s</math> is a random variable but unlike Fisher they did not assume that they knew its distribution but rather used an imperical distribution obtained from the data. They then consider a second sample with sample size a multiple t of the first sample and calcultate the expected number of words that will occur in this sample that did not occur in the first sample. They find that if they take a sample the size of his known works the expected number of new words would be 11,430 which can be considered to be a lower bound on the number of additional words that Shakespeare knew. | ||
| Line 328: | Line 327: | ||
expected cummulative number of species from the model;(.....), successive estimates of the maximum number of species > 2m long.</blockquote>. | expected cummulative number of species from the model;(.....), successive estimates of the maximum number of species > 2m long.</blockquote>. | ||
===Reverences=== | |||
(1) Fisher R.A.; Corbet; C.B. Williams C.B. (1943), The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population." '' Journal of Animal Ecology'', 12, 42-58. (Available from Jstor). | |||
(2) Good, I. J (1953) "On the population freqencies of species and the estimation of population parameters," ''Biometrika'', 40, 2137-264. | |||
(3) Good I.J. and Toulmin (G) (1956) "The number of new species, and the increase in population coverage when a sample is increased", ''Biometrika'', 43, 45-63. | |||
Thisted, R., and Efron, B (1976) "Estimating the Number of unseen species: How many words did Shakespeare know?" ''Biometrika, 63,(1976) 435-447. | |||
Thisted, R, and Efron, B (1987), "Did Shakespear write a newly discovered poem?" ''Biometrika'', 74 (1986), 445, 445-455 . | |||
To be continued | To be continued | ||
Revision as of 19:27, 2 December 2006
Quotation
It would be hard to make a probability course boring.
William Feller
Personal comment to Laurie Snell
Forsooth
The following Forsooths are from the November 2006 RRS NEWS.
At St John's Wood station alone, the number of CCTV cameras has jumped from 20 to 57, an increase of 300 per cent.
Metro
3 May 2006
Now 78% of female veterinary medicine students are women, almost a complete turn-around from the previous situation.
The Herald (Glasgow)
4 May 2006
Drought to ravage half the world within 100 years
Half the world's surface will be gripped by drought by the end of the century, the Met Office said yesterday.
Times online
6 October 2006
I wasn't making up data, I was imputing!
An Unwelcome Discovery, by Jeneen Interlandi, The New York Times, October 22, 2006.
The New York Times has an informative summary of a recent scandal involving a prominent researcher at the University of Vermont, Eric Poehlman. The Poehlman scandal represents perhaps the biggest cases of research fraud in recent history.
He presented fraudulent data in lectures and in published papers, and he used this data to obtain millions of dollars in federal grants from the National Institutes of Health — a crime subject to as many as five years in federal prison.
The first person to speak up about the possibility of fraud in Poehlman's work was one of his research assistants, Walter DeNino.
The fall that DeNino returned to the lab, Poehlman was looking into how fat levels in the blood change with age. DeNino’s task was to compare the levels of lipids, or fats, in two sets of blood samples taken several years apart from a large group of patients. As the patients aged, Poehlman expected, the data would show an increase in low-density lipoprotein (LDL), which deposits cholesterol in arteries, and a decrease in high-density lipoprotein (HDL), which carries it to the liver, where it can be broken down. Poehlman’s hypothesis was not controversial; the idea that lipid levels worsen with age was supported by decades of circumstantial evidence. Poehlman expected to contribute to this body of work by demonstrating the change unequivocally in a clinical study of actual patients over time. But when DeNino ran his first analysis, the data did not support the premise.
When Poehlman saw the unexpected results, he took the electronic file home with him. The following week, Poehlman returned the database to DeNino, explained that he had corrected some mistaken entries and asked DeNino to re-run the statistical analysis. Now the trend was clear: HDL appeared to decrease markedly over time, while LDL increased, exactly as they had hypothesized.
Although DeNino trusted his boss implicitly, the change was too great to be explained by a handful of improperly entered numbers, which was all Poehlman claimed to have fixed. DeNino pulled up the original figures and compared them with the ones Poehlman had just given him. In the initial spreadsheet, many patients showed an increase in HDL from the first visit to the second. In the revised sheet, all patients showed a decrease. Astonished, DeNino read through the data again. Sure enough, the only numbers that hadn’t been changed were the ones that supported his hypothesis.
Poehlman brushed DeNino's concerns aside, so DeNino started asking around and other graduate students and postdocs had similar concerns. He got some cautionary advice from a former postdoctoral fellow
Being associated with either falsified data or a frivolous allegation against a scientist as prominent as Poehlman could end DeNino’s career before it even began.
and a faculty member who shared lab space with Poehlman who advised
If you’re going to do something, make sure you really have the evidence.
So DeNino started looking for the evidence.
DeNino spent the next several evenings combing through hundreds of patients’ records in the lab and university hospital, trying to verify the data contained in Poehlman’s spreadsheets. Each night was worse than the one before. He discovered not only reversed data points, but also figures for measurements that had never been taken and even patients who appeared not to exist at all.
DeNino presented his evidence to the university counsel and the response of Poehlman (to his department chair, Burton Sobel) was rather startling.
The accused scientist gave him the impression that nothing was wrong and seemed mostly annoyed by all the fuss. In his written response to the allegations, Poehlman suggested that the data had gotten out of hand, accumulating numerous errors because of handling by multiple technicians and postdocs over the years. “I found that noncredible, really, for an investigator of Eric’s experience,” Sobel later told the investigative panel. “There had to be a backup copy that was pure,” Sobel reasoned before the panel. “You would not have postdocs and lab techs in charge of discrepant data sets.” But Poehlman told Sobel that there was no master copy.
At the formal hearing, Poehlman had a different defense.
First, he attributed his mistakes to his own self-proclaimed ineptitude with Excel files. Then, when pressed on how fictitious numbers found their way into the spreadsheet he’d given DeNino, Poehlman laid out his most elaborate explanation yet. He had imputed data — that is, he had derived predicted values for measurements using a complicated statistical model. His intention, he said, was to look at hypothetical outcomes that he would later compare to the actual results. He insisted that he never meant for DeNino to analyze the imputed values and had given him the spreadsheet by mistake.
The New York Times article points out how pathetic this attempted explanation was.
Although data can be imputed legitimately in some disciplines, it is generally frowned upon in clinical research, and this explanation came across as hollow and suspicious, especially since Poehlman appeared to have no idea how imputation was done.
A large portion of the article examines how research fraud can occur in a system that is supposed to be self-correcting.
First, the people who are mostly likely to notice fraud are junior investigators who are subordinate to their research mentor. It's psychologically and emotionally difficult to confront someone who has devoted time to your professional development. Even when an investigator is emotionally willing to confront their mentor, they have their career concerns to worry about.
The principal investigator in a lab has the power to jump-start careers. By writing papers with graduate students and postdocs and using connections to help obtain fellowships and appointments, senior scientists can help their lab workers secure coveted tenure-track jobs. They can also do damage by withholding this support.
Every university will have a system in place to investigate claims of fraud. But there are problems here as well.
All universities that receive public money to conduct research are required to have an integrity officer who ensures compliance with federal guidelines. But policing its scientists can be a heavy burden for a university. “It’s your own faculty, and there’s this idea of supporting and nurturing them,” says Ellen Hyman-Browne, a research-compliance officer at the Children’s Hospital of Philadelphia, a teaching hospital. Moreover, investigations cost time and money, and no institution wants to discover something that could cast a shadow on its reputation.
“There are conflicting influences on a university where they are the co-grantor and responsible to other investigators,” says Stephen Kelly, the Justice Department attorney who prosecuted Poehlman. “For the system to work, the university has to be very ethical.”
Poehlman himself was careful and chose areas where fraud would be especially difficult to detect. He specialized in presenting longitudinal data, data that is very expensive to replaicate. He also presented research results that confirmed what most researchers had suspected, rather than results that would undermine existing theories of nutrition.
At his sentencing, Poehlman was sentenced to one year and one day in federal prison, making him the first researcher to serve time in jail for research fraud.
“When scientists use their skill and their intelligence and their sophistication and their position of trust to do something which puts people at risk, that is extraordinarily serious,” the judge said. “In one way, this is a final lesson that you are offering.”
Questions
1. Do you have experience with a researcher changing the data values after seeing the initial analysis results? What would make you suspicious of fraud?
2. Is the peer-review system of research self-correcting? What changes could be made to this system?
3. When is imputation legitimate and when is it fraudulent?
Submitted by Steve Simon</math>
Independence for national statistics
A better way to restore faith in official statistics, John Kay, Financial Times 25 July 2006.
John Kay, a columnist for the Financial Times, outlines the measures needed to ensure that national statistics are truly independent.
The current state of UK official statistics was covered in a previous Chance article Pick a number, any number, in Chance News 9. That article summarised a report on this topic, to which professional users, such the Royal Statistical Society, gave a cautious welcome to the government’s announcement of independence for the UK Office of National Statistics (ONS).
Kay's article follows up on the reaction to that report. He tells us that accurate public information is a prerequisite of democracy, governement statisticians are honest people but ministers (politicians) needs are often for propaganda rather than facts. Kay claims that decentralisation of responsibility for the production of official statistics has created a two-tier system in the UK.
statistics produced by the Office for National Statistics (ONS), which operates to internationally agreed criteria, are of higher quality than those produced by (government) departments.
The proposal to hand repsonsibility for all official statistics to the ONS was rejected, as were the suggestions for greater independence, made by bodies such as the Statistics Commission and the Royal Statistical Society,
- separating statistical information from political statements,
- reducing access by ministers to new data before their release,
- giving parliament a defined role in the appointment of the National Statistician.
Instead, the lastest news is that the ONS will be demoted to a non-ministerial department. The worst news is the abolition of the Statistics Commission, which reviews all government statistics, and has made itself unpopular with government by proving itself robustly independent.
Kay also cautions that statistics may be misused in contexts other than those intended. The value of health services increases as incomes rise and it can be argued that this increases the value of health output even if outcomes and procedures are unchanged. This statistical adjustment provides no basis whatever for claims that the National Health Service is more efficient. But the assertion grabs a headline, and it is only much later that pedantic journalists and academics can discover what is actually going on.
Submitted by John Gavin.
Estimating the diversity of dinosaurs
Proceedings of the National Academy of Sciences
Published online before print September 5, 2006
Steve C. Wang, and Peter Dodson
Fossil hunters told: Dig deeper
Philadelphia Inquirer, September 5, 2006
Tom Avril
Steve Wang is a statistician at Swarthmore College and Peter Dodson is a paleontologist at the University of Pennsylvania. Their study was widely reported in the media. You can find references to the media coverage and comments by Steve here.
In their paper the authors provided the following description of their results. Here are a few definitions that might be helpful: genera: a collective term used to incorporate like-species into one group, nonavian: not derived from birds, fossiliferous: containing a fossil, rock outcrop: the part of a rock formation that appears above the surface of the surrounding land
Despite current interest in estimating the diversity of fossil and extant groups, little effort has been devoted to estimating the diversity of dinosaurs. Here we estimate the diversity of nonavian dinosaurs at 1,850 genera, including those that remain to be discovered. With 527 genera currently described, at least 71% of dinosaur genera thus remain unknown. Although known diversity declined in the last stage of the Cretaceous, estimated diversity was steady, suggesting that dinosaurs as a whole were not in decline in the 10 million years before their ultimate extinction. We also show that known diversity is biased by the availability of fossiliferous rock outcrop. Finally, by using a logistic model, we predict that 75% of discoverable genera will be known within 60-100 years and 90% within 100-140 years. Because of nonrandom factors affecting the process of fossil discovery (which preclude the possibility of computing realistic confidence bounds), our estimate of diversity is likely to be a lower bound.
In this problem we have a sample of dinosaurs that lived on the earth. These dinosaurs are classified into groups called genera. We can count the number of each generus in our sample. From this we want to estimate the total number of dinosaurs that have roamed the earth. Many different methods for doing this have been developed and the authors of this study use one of the newer methods. We have discussed in prevent Chance News other examples of this problem and it might help to discuss these briefly.
One of the first studies of this kind was suggested by asking similar questions about the number of different species of butterflies in Malaya and was reported in the paper "The Relation Between the Number of Species and the Number of Individuals in 1943 in a paper by R.A. Fisher, A.A. Corbet and C. B. Williams.(1)
The authors write:
It is the usual experience of collectors of species in a biological group that the species are not equally abundant, even under conditions of considerable uniformity, a majority being comparatively rare while only a few are common. As far as we are aware, no suggestion has been made previously that any mathematical relation existes between the number of individuals and the nummber of species in a random sample of insects or other animals.
Fisher assumed that for a given sample size the number of occurrences of the jth species has a Poisson distribution with mean <math>\lambda_j</math>, and the <math>\lambda_j s</math> are independent random variables having a Gamma distribution so the compound distribution is negative binomial distribution . This distribution is truncated to take into account that the number of species with 0 occurrances is not known. Finally Fisher took a limiting form of this distribution which resulted in logarithmic distribution from which the expected number of species with n individuals is found to be:
<math>\frac{\alpha}{n}x^n. </math> where <math>\alpha </math> and x are parameters obtained as solutions of the equations:
<math> S = -\alpha log_e(1-x), N = \frac{\alpha x}{(1-x)}.</math> where S is the sample size and N the number of species observed.
Recall that
<math>log_e(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}, ..., etc. </math> From this it follows that the total number of species expected is:
<math>\sum_{n=1}^{\infty} \frac{\alpha}{n} = -\alpha log_e(1-x).</math> It is also easy to see that the total number of individuals expected is
<math>\sum_{n=1}^{\infty} \alpha x^n = -\frac{\alpha x}{1-x}</math> For the data provided for the Malayan butterflies the total sample size S was 9031 and the number of species observed was 620. Using these values the authors found x = .997 and <math>\alpha = 135.46.</math> Using these values they obtained <math>\alpha</math> resulting in the following table with n is the number of times that a species occurs.
Wang and Dodson were interested in finding the number of species (in their case genera) that have not been observed in previous samples. This problem was first studied in 1953 by I. J. Good (2) and in 1956 by I.J. Goode and G. H. Tollmin (3) Bradley Efron and Ronals Thisted used the methods developed by Good and Tollmin to answer two questions provided in the titles of the two papers they wrote; Efron and Thisted considered the words in Shakespeare's as species and took as the first sample Shakespear's know works which comprised of 884,647 using their convention when two words are different they found 31,534 different words. The provided a table showing the number of words that accored once, twice, three times ect. up to 100. Following Fisher they assumed that for the first sample the number of times that a word occurs s has a Poisson distribution with mean <math>\lambda_s</math> which is proportional to the size of the sample. Like Fisher they assumed that <math>\lambda_s</math> is a random variable but unlike Fisher they did not assume that they knew its distribution but rather used an imperical distribution obtained from the data. They then consider a second sample with sample size a multiple t of the first sample and calcultate the expected number of words that will occur in this sample that did not occur in the first sample. They find that if they take a sample the size of his known works the expected number of new words would be 11,430 which can be considered to be a lower bound on the number of additional words that Shakespeare knew.
In their second paper Efron and Thisted use their results to help decide if a new poem found in 1985 by Shakesperean scholar Gary Taylor was written by Shakespeare. This poem had 429 words with 258 being distinct. The authors ranked the 258 distinct words in order of rairity of usage in Shakespeares known works. They found that 9 of the words were never used by Shakespeare. They estimated that if Shakespeare were to write new work with 429 words the expected number of new words would be 6.97. They develop other similar tests and apply them to this new poem as well as to similar size poems known to be written by well known authors of the same period as Shakspeare. They conclude "On balance, the poem is found to fit previous Shakespearean usage reasonably well.
Another way to look the prolem of estimating the number of species not yet observed is illustrated was discussed in [http://www.dartmouth.edu/~chance/chance_news/recent_news/chance_news_7.06.html#Hidden%20truths Chance News 7.06.
Here we discussed research by Charles Paxton of Oxford University, who statistics estimated the number of yet undiscovered salt water species whose length exceeds 2 meters. By 1995, the number of such species identified had reached 217, but the rate of new finds has been decreasing. By examining the pattern of discoveries over the years 1830-1995, Paxton estimates that 47 such species remain to be found. He did this by constructing the following species accumulation curve for these large marine animals from 1830 to 1995.
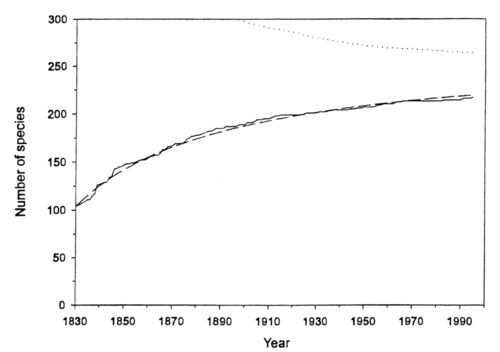
Number of described large open water fauna (>2m length/width)
since 1830 (-), cummulative number of species discribed;(-----), the
expected cummulative number of species from the model;(.....), successive estimates of the maximum number of species > 2m long.
.
Reverences
(1) Fisher R.A.; Corbet; C.B. Williams C.B. (1943), The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population." Journal of Animal Ecology, 12, 42-58. (Available from Jstor).
(2) Good, I. J (1953) "On the population freqencies of species and the estimation of population parameters," Biometrika, 40, 2137-264.
(3) Good I.J. and Toulmin (G) (1956) "The number of new species, and the increase in population coverage when a sample is increased", Biometrika, 43, 45-63.
Thisted, R., and Efron, B (1976) "Estimating the Number of unseen species: How many words did Shakespeare know?" Biometrika, 63,(1976) 435-447.
Thisted, R, and Efron, B (1987), "Did Shakespear write a newly discovered poem?" Biometrika, 74 (1986), 445, 445-455 .
To be continued